Hàm SIN và hàm SINH trong Excel có tên gọi gần giống nhau, nhưng phục vụ các mục đích toán học hoàn toàn khác nhau. SIN dùng để tính giá trị lượng giác thông thường của góc, trong khi SINH tính giá trị lượng giác hyperbolic của số. Sự nhầm lẫn này khiến nhiều người dùng áp dụng sai hàm, dẫn đến kết quả không chính xác trong phép tính.
Hàm SIN: Lượng Giác Cơ Bản Cho Góc
Hàm SIN trả về giá trị sine của một góc được biểu diễn bằng radian. Đây là hàm lượng giác thông thường mà bạn học từ trung học, áp dụng trên đường tròn lượng giác.
Cú pháp:
=SIN(number)Trong đó:
number: Góc tính bằng radian mà bạn muốn tính sine- Để chuyển độ sang radian: nhân với
PI()/180hoặc dùng hàmRADIANS()
Các ví dụ thực tế:
Tính sine của 30 độ:
=SIN(RADIANS(30))Kết quả: 0.5
Tính sine của π/2 radian:
=SIN(PI()/2)Kết quả: 1
Tính sine của 45 độ:
=SIN(PI()/4)Kết quả: 0.707 (xấp xỉ √2/2)
Hàm SIN có giá trị nằm trong khoảng từ -1 đến 1. Điều này phản ánh thực tế rằng trên đường tròn đơn vị, tọa độ y của điểm luôn nằm trong phạm vi này. Kết quả lặp lại sau mỗi chu kỳ 2π, do tính chất tuần hoàn của hàm sine.
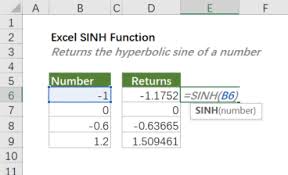
Hàm SINH: Lượng Giác Hyperbolic Cho Phương Trình
Hàm SINH tính giá trị sine hyperbolic của một số, dựa trên hàm số mũ. Khác với SIN hoạt động trên đường tròn, SINH hoạt động trên đường hyperbola với phương trình x² – y² = 1.
Cú pháp:
=SINH(number)Trong đó:
number: Giá trị số thực bất kỳ (không phải góc, không cần đổi đơn vị)
Công thức toán học:
SINH(x) = (e^x - e^-x) / 2Trong đó e là hằng số Euler (khoảng 2.71828).
Các ví dụ thực tế:
Tính SINH của 1:
=SINH(1)Kết quả: 1.175 (tương đương (e¹ – e⁻¹)/2)
Tính SINH của 0:
=SINH(0)Kết quả: 0 (vì (e⁰ – e⁰)/2 = 0)
Tính SINH của -2:
=SINH(-2)Kết quả: -3.627 (hàm SINH là hàm lẻ, nên SINH(-x) = -SINH(x))
Không giống SIN, hàm SINH không bị giới hạn trong khoảng -1 đến 1. Giá trị của SINH có thể tăng lên vô hạn khi x tăng, và giảm xuống âm vô hạn khi x giảm. Đây là điểm khác biệt quan trọng nhất giữa hai hàm.
So Sánh Trực Tiếp: SIN vs SINH
Để thấy rõ sự khác biệt, hãy tính cả hai hàm với cùng giá trị đầu vào.
Với giá trị 1:
=SIN(1) → 0.841
=SINH(1) → 1.175Với giá trị 2:
=SIN(2) → 0.909
=SINH(2) → 3.627Với giá trị 5:
=SIN(5) → -0.959
=SINH(5) → 74.203Sự chênh lệch tăng theo cấp số nhân khi giá trị đầu vào lớn lên. Ở giá trị 5, SINH lớn hơn SIN gần 80 lần. Với giá trị 10, chênh lệch lên đến hàng nghìn lần. Điều này cho thấy hai hàm phục vụ các mục đích toán học hoàn toàn khác nhau.
Ứng Dụng Thực Tế Của SIN
Hàm SIN xuất hiện trong các tính toán liên quan đến:
Dao động và sóng: Tính biên độ sóng âm thanh, sóng ánh sáng, hoặc dao động điều hòa. Ví dụ: tính độ cao của sóng biển tại thời điểm t giây.
Góc và tam giác: Giải các bài toán tam giác trong trắc địa, kiến trúc. Tính chiều cao của tòa nhà dựa vào góc quan sát và khoảng cách.
Quay vòng và chu kỳ: Mô phỏng chuyển động tròn, bánh xe, hoặc bất kỳ chuyển động tuần hoàn nào. Ví dụ: tính vị trí của kim giờ trên đồng hồ.
Tín hiệu điện: Phân tích dạng sóng AC, sóng radio, hoặc tín hiệu điện tử. Tính điện áp tức thời trong mạch xoay chiều.
Ứng Dụng Thực Tế Của SINH
Hàm SINH xuất hiện trong các bài toán phức tạp hơn:
Đường cáp treo (Catenary): Tính hình dạng của dây cáp điện cao thế treo giữa hai trụ. Công thức: y = a×cosh(x/a), trong đó cosh liên quan trực tiếp đến sinh. Kỹ sư điện dùng công thức này để tính độ dài dây cần thiết, đảm bảo dây không căng quá gây đứt hoặc chùng quá gây nguy hiểm.
Phương trình vi phân: Giải các phương trình mô tả truyền nhiệt, động lực học chất lỏng. Nghiệm thường chứa sinh và cosh.
Vật lý tương đối: Mô tả biến đổi Lorentz trong thuyết tương đối hẹp của Einstein. Tính toán về vận tốc gần tốc độ ánh sáng.
Mô hình sóng phi tuyến: Mô tả sóng soliton, front phản ứng khuếch tán trong hóa học và sinh học. Các nghiệm chứa tanh (liên quan đến sinh).
Hình học hyperbolic: Tính toán trong không gian phi Euclid, ứng dụng trong đồ họa máy tính và mạng nơ-ron.
Tôi chỉ cần hàm SINH khi làm việc với các bài toán kỹ thuật cao cấp. Đối với hầu hết người dùng Excel văn phòng, SIN là lựa chọn phù hợp cho các tính toán lượng giác thông thường.
Công Thức Kết Hợp SIN và SINH
Có những công thức toán học kết nối hai hàm này thông qua số phức:
Công thức Euler cho số phức:
sin(ix) = i × sinh(x)
sinh(ix) = i × sin(x)Trong đó i là đơn vị ảo (i² = -1), x là số thực.
Tuy nhiên, Excel không hỗ trợ trực tiếp số phức với các hàm lượng giác cơ bản. Bạn cần dùng các hàm kỹ thuật (Engineering functions) như IMSIN, IMSINH nếu làm việc với số phức.
Các Hàm Liên Quan
Cả SIN và SINH đều có các hàm bổ trợ:
Họ hàm lượng giác thông thường:
- COS(x): Cosine
- TAN(x): Tangent
- ASIN(x): Arcsine (nghịch đảo của SIN)
Họ hàm lượng giác hyperbolic:
- COSH(x): Cosine hyperbolic
- TANH(x): Tangent hyperbolic
- ASINH(x): Arcsine hyperbolic (nghịch đảo của SINH)
Các cặp hàm này có mối quan hệ tương tự nhau. Ví dụ:
sin²(x) + cos²(x) = 1 (Đường tròn)
cosh²(x) - sinh²(x) = 1 (Đường hyperbola)Lỗi Thường Gặp Và Cách Khắc Phục
Lỗi #NUM! với SIN: Xảy ra khi giá trị quá lớn khiến Excel không thể tính toán. Hàm SIN chấp nhận mọi số thực, nhưng với số cực lớn, độ chính xác giảm.
Quên đổi độ sang radian:
❌ SAI: =SIN(30) → Cho 30 radian, không phải 30 độ
✅ ĐÚNG: =SIN(RADIANS(30)) → Cho 30 độNhầm lẫn SIN với SINH trong công thức: Nếu kết quả bạn nhận được vượt quá khoảng -1 đến 1 trong bài toán góc, bạn có thể đã dùng nhầm SINH thay vì SIN.
Dùng SINH cho bài toán góc:
❌ SAI: =SINH(RADIANS(45)) → Không có ý nghĩa
✅ ĐÚNG: =SIN(RADIANS(45)) → Tính sine của 45 độSINH không nhận góc làm đầu vào. Nó nhận số thực bất kỳ và tính theo công thức hàm mũ.
Bảng Tra Cứu Nhanh
| Tiêu chí | SIN | SINH |
|---|---|---|
| Mục đích | Lượng giác thông thường | Lượng giác hyperbolic |
| Đầu vào | Góc (radian) | Số thực bất kỳ |
| Khoảng giá trị | -1 đến 1 | -∞ đến +∞ |
| Tính tuần hoàn | Có (chu kỳ 2π) | Không |
| Công thức | Định nghĩa hình học | (e^x – e^-x) / 2 |
| Ứng dụng | Góc, sóng, dao động | Dây cáp treo, phương trình vi phân |
| Excel version | Tất cả | Excel 2003 trở lên |
Khi Nào Dùng Hàm Nào
Chọn SIN khi:
- Tính toán liên quan đến góc (tam giác, hình học)
- Mô phỏng chuyển động tròn hoặc dao động
- Xử lý tín hiệu tuần hoàn (sóng, âm thanh)
- Làm việc với độ hoặc radian
Chọn SINH khi:
- Giải phương trình vi phân phi tuyến
- Tính hình dạng dây cáp treo (catenary)
- Làm việc với hàm mũ phức tạp
- Mô hình hóa tăng trưởng hoặc suy giảm phi tuyến
Đối với 95% người dùng Excel trong môi trường văn phòng, SIN là lựa chọn phù hợp. SINH xuất hiện chủ yếu trong các lĩnh vực kỹ thuật chuyên sâu như cơ khí, điện, vật lý, và toán học ứng dụng.
Kiểm Tra Nhanh: Bạn Cần Hàm Nào?
Trả lời các câu hỏi sau để xác định:
- Bài toán của bạn có liên quan đến góc? → Dùng SIN
- Công thức chứa e^x hoặc hàm mũ? → Dùng SINH
- Giá trị mong đợi nằm trong -1 đến 1? → Dùng SIN
- Đang giải phương trình y” = y? → Dùng SINH (nghiệm có dạng A×sinh + B×cosh)
- Tính tọa độ trên đường tròn? → Dùng SIN
- Tính hình dạng dây cáp? → Dùng SINH (thông qua COSH)
Tài Nguyên Học Thêm
Cả hai hàm đều có trong Excel từ phiên bản 2003 trở đi. Excel 365 và các phiên bản mới nhất hỗ trợ đầy đủ cả hai họ hàm lượng giác thông thường và hyperbolic.
Để thực hành, bạn có thể tạo bảng giá trị từ -5 đến 5 và so sánh kết quả của SIN(x) và SINH(x). Điều này giúp bạn hình dung rõ ràng sự khác biệt về đồ thị và giá trị giữa hai hàm.
Nếu làm việc với các bài toán phức tạp hơn, tham khảo thêm về các hàm kỹ thuật (Engineering functions) trong Excel, bao gồm các hàm xử lý số phức, chuyển đổi đơn vị, và tính toán Bessel.