Hàm DEVSQ Trong Excel: Cách Tính Độ Phân Tán Dữ Liệu Chỉ Trong 1 Công Thức

Phân tích độ phân tán của dữ liệu thường yêu cầu nhiều bước tính toán phức tạp. Tính trung bình của dãy số, lấy từng giá trị trừ đi trung bình, bình phương kết quả, rồi cộng tất cả lại. Với tập dữ liệu lớn, quy trình này tốn hàng chục phút. Hàm DEVSQ tự động hóa toàn bộ quá trình này trong một công thức duy nhất.

Mục Lục

DEVSQ Là Gì Và Cách Hoạt Động

Hàm DEVSQ tính tổng bình phương độ lệch của các điểm dữ liệu so với giá trị trung bình của chúng. Đây là một trong những hàm thống kê cốt lõi giúp đo lường sự biến động trong tập dữ liệu.

Cú pháp cơ bản:

=DEVSQ(number1, [number2], ...)

Các tham số:

number1: Bắt buộc, có thể là số, tham chiếu ô, hoặc dải ô
number2, …: Tùy chọn, tối đa 255 tham số

Hàm này thực hiện bốn bước tự động. Đầu tiên, tính giá trị trung bình của toàn bộ dãy số. Tiếp theo, lấy từng số trừ đi giá trị trung bình để có độ lệch. Sau đó, bình phương từng độ lệch. Cuối cùng, cộng tất cả các giá trị bình phương lại.

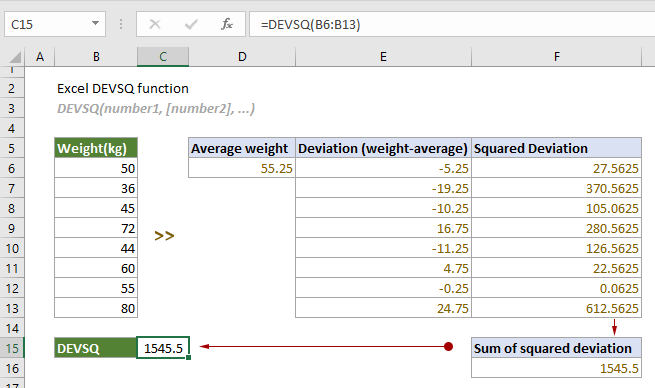
XEM THÊM: Tôi Mất 30 Phút Tính Xác Suất Chuẩn Cho Đến Khi Phát Hiện Hàm GAUSS

Ví dụ cụ thể: Với dãy số 2, 5, 8, 11, 14 trong ô A1:A5, công thức =DEVSQ(A1:A5) trả về 110. Giá trị trung bình là 8. Các độ lệch lần lượt là -6, -3, 0, 3, 6. Bình phương các độ lệch ra 36, 9, 0, 9, 36. Tổng là 110.

Tại Sao DEVSQ Nhanh Hơn Cách Thủ Công

Cách tính truyền thống yêu cầu tối thiểu năm bước riêng biệt. Tạo cột tính trung bình bằng hàm AVERAGE. Tạo cột mới để trừ từng giá trị cho trung bình. Thêm cột thứ ba để bình phương các độ lệch. Sử dụng hàm SUM cho cột bình phương. Cuối cùng định dạng lại các cột để dễ đọc.

So sánh hiệu suất:

Phương pháp thủ công với 100 dòng dữ liệu: 5 phút để tạo công thức và định dạng
DEVSQ với cùng dữ liệu: 10 giây để nhập công thức
Tiết kiệm: 98% thời gian

Hàm DEVSQ còn tự động loại bỏ giá trị văn bản và ô trống, chỉ tính các ô chứa số. Ô có giá trị 0 vẫn được tính. Điều này giúp tránh lỗi thường gặp khi sử dụng phương pháp thủ công.

DEVSQ Khác Gì VAR Và STDEV

Nhiều người nhầm lẫn giữa DEVSQ với các hàm phương sai và độ lệch chuẩn. Sự khác biệt nằm ở bước cuối cùng trong công thức.

Mối liên hệ:

DEVSQ: Tổng bình phương độ lệch (không chia cho n)
VAR.S: DEVSQ chia cho (n-1) để có phương sai mẫu
STDEV.S: Căn bậc hai của VAR.S để có độ lệch chuẩn

XEM THÊM: Dự Báo Doanh Thu Chính Xác Với Hàm FORECAST.ETS Excel 2016

Với dãy 10 số, DEVSQ trả về 500. VAR.S trả về 55.56 (500 chia 9). STDEV.S trả về 7.45 (căn bậc hai của 55.56). Ba hàm phục vụ mục đích khác nhau trong phân tích thống kê.

Khi nào dùng DEVSQ:

Tính phương sai thủ công khi cần kiểm soát mẫu hay tổng thể
Kết hợp với các hàm khác để tính toán nâng cao
Phân tích hồi quy tuyến tính và các mô hình thống kê

Ứng Dụng Thực Tế Trong Phân Tích Dữ Liệu

Phân tích điểm thi của lớp học

Giáo viên có danh sách điểm 40 học sinh từ 0 đến 100. Sử dụng DEVSQ giúp đánh giá mức độ đồng đều của điểm số.

Công thức =DEVSQ(B2:B41) trả về 18500. Chia cho 39 học sinh (n-1) để có phương sai 474.36. Độ lệch chuẩn là 21.78 điểm. Con số này cho thấy khoảng cách điểm giữa các học sinh khá lớn, cần điều chỉnh phương pháp giảng dạy.

Theo dõi doanh số bán hàng hàng tháng

Doanh nghiệp cần đánh giá sự ổn định của doanh thu qua 12 tháng. Doanh số dao động từ 50 triệu đến 120 triệu mỗi tháng.

Sử dụng =DEVSQ(C2:C13) cho dữ liệu doanh thu. Kết quả 28000000000 cho thấy sự biến động cao. So sánh với quý trước để thấy xu hướng cải thiện hay xấu đi. Giá trị DEVSQ giảm theo thời gian chứng tỏ doanh số đang ổn định hơn.

Kiểm soát chất lượng sản xuất

Nhà máy đo kích thước sản phẩm với tiêu chuẩn 50mm, sai số cho phép 0.5mm. Thu thập 200 mẫu mỗi ngày để kiểm tra.

XEM THÊM: Hàm AVERAGE Excel: Sau 3 Năm Tính Trung Bình Sai, Tôi Mới Biết Điều Này

Công thức =DEVSQ(D2:D201) cho biết tổng bình phương độ lệch. Nếu giá trị tăng đột ngột so với ngày trước, máy móc có thể cần bảo trì. Phương pháp này giúp phát hiện vấn đề sớm trước khi sản xuất hàng loạt sản phẩm lỗi.

Kết Hợp DEVSQ Với Các Hàm Khác

Tính hệ số biến thiên

Hệ số biến thiên đo mức độ phân tán tương đối của dữ liệu. Công thức kết hợp SQRT, DEVSQ, COUNT và AVERAGE.

=SQRT(DEVSQ(A1:A100)/(COUNT(A1:A100)-1))/AVERAGE(A1:A100)*100

Kết quả là phần trăm, dễ so sánh giữa các tập dữ liệu có đơn vị khác nhau. Doanh thu và chi phí có thể so sánh độ ổn định dựa trên hệ số này.

Xác định giá trị ngoại lệ

Giá trị ngoại lệ thường nằm xa giá trị trung bình hơn ba lần độ lệch chuẩn. Sử dụng DEVSQ để tính ngưỡng này.

=AVERAGE(A1:A100) + 3*SQRT(DEVSQ(A1:A100)/(COUNT(A1:A100)-1))

Bất kỳ giá trị nào vượt ngưỡng này cần kiểm tra lại. Phương pháp này hữu ích trong phân tích dữ liệu tài chính và khoa học.

Lưu Ý Quan Trọng Khi Sử Dụng

Hàm DEVSQ chỉ hoạt động với dữ liệu số. Nếu dải ô chứa văn bản hoặc giá trị logic trong tham chiếu, những giá trị này bị bỏ qua tự động. Nhưng nếu nhập trực tiếp văn bản vào đối số hàm, Excel trả về lỗi giá trị.

Lỗi thường gặp:

Lỗi giá trị khi dải ô trống hoàn toàn
Lỗi tham số nếu gõ text trực tiếp vào hàm
Kết quả 0 nếu tất cả giá trị giống nhau

Hàm này có sẵn trong mọi phiên bản Excel từ 2007 trở đi, bao gồm Excel 365, Excel 2021, Excel 2019 và Excel 2016. Cũng hoạt động trong Google Sheets và LibreOffice Calc với cú pháp tương tự. Đối với phân tích phương sai nâng cao, cân nhắc sử dụng công cụ phân tích dữ liệu trong tab Data.