5 Bước Sử Dụng Hàm T.DIST.RT Thay Thế Bảng Tra Giá Trị Tới Hạn

Tôi từng mất 10 phút mỗi lần tra bảng giá trị tới hạn phân bố Student. Phải tìm đúng hàng bậc tự do, đúng cột mức ý nghĩa, rồi đọc giá trị giao nhau. Sai một bước là kết quả kiểm định sai hoàn toàn. Hàm T.DIST.RT trong Excel thay đổi toàn bộ quy trình này chỉ trong vài giây.

Mục Lục

Bước 1: Hiểu cú pháp cơ bản của hàm

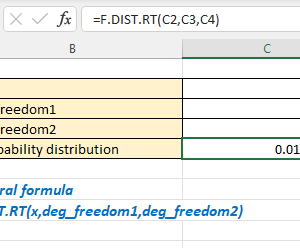
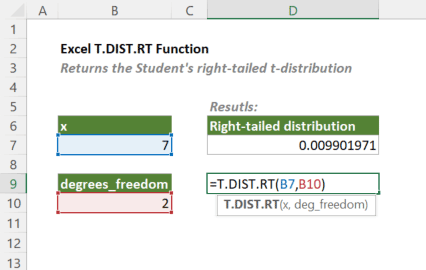
Hàm T.DIST.RT tính xác suất đuôi bên phải của phân bố t-Student. Công thức chỉ cần hai tham số đơn giản.

Cú pháp:

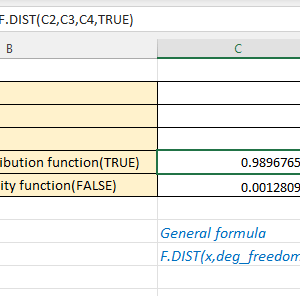
=T.DIST.RT(x, deg_freedom)

x: Giá trị thống kê t cần tính xác suất
deg_freedom: Số bậc tự do, phải là số nguyên dương

Ví dụ đơn giản nhất: =T.DIST.RT(2.5, 10) trả về 0.0158. Con số này có nghĩa xác suất quan sát được giá trị t lớn hơn 2.5 với 10 bậc tự do là 1.58 phần trăm.

Hàm này hoạt động từ Excel 2010 trở lên. Nếu bạn dùng phiên bản cũ hơn, phải dùng hàm TDIST với tham số tails bằng 1. Cú pháp cũ phức tạp hơn và dễ nhầm lẫn.

Bước 2: Xác định giá trị x từ dữ liệu mẫu

Giá trị x không phải số tùy ý mà đến từ công thức kiểm định t-test. Với kiểm định giả thuyết về trung bình một mẫu, công thức tính t là:

Công thức t-statistic:

t = (x̄ - μ₀) / (s / √n)

Trong đó:

x̄: Trung bình mẫu
μ₀: Giá trị trung bình giả thiết
s: Độ lệch chuẩn mẫu
n: Kích thước mẫu

Ví dụ thực tế: Kiểm tra xem trung bình điểm thi của một lớp có lớn hơn 70 điểm không. Mẫu 15 sinh viên, điểm trung bình 74, độ lệch chuẩn 8.

t = (74 - 70) / (8 / √15)
t = 4 / 2.066
t = 1.936

Giá trị t này chính là tham số x cho hàm T.DIST.RT. Trong tình huống khác như so sánh hai mẫu, công thức t phức tạp hơn nhưng nguyên tắc giống nhau.

XEM THÊM: Nếu Dữ Liệu Có Text và TRUE/FALSE, Bạn Cần Hàm VARA Không Phải VAR

Bước 3: Tính bậc tự do chính xác

Bậc tự do quyết định hình dạng phân phối t-Student. Công thức thay đổi tùy loại kiểm định.

Một mẫu:

df = n - 1

Với ví dụ 15 sinh viên ở trên, df = 15 – 1 = 14.

Hai mẫu độc lập với phương sai bằng nhau:

df = n₁ + n₂ - 2

Hai mẫu độc lập với phương sai khác nhau (Welch’s t-test):

df = [(s₁²/n₁ + s₂²/n₂)²] / [(s₁²/n₁)²/(n₁-1) + (s₂²/n₂)²/(n₂-1)]

Công thức này phức tạp và thường cho ra số thập phân. Excel tự động làm tròn xuống số nguyên khi bạn nhập vào hàm. Ví dụ df = 18.7 sẽ trở thành 18.

Lưu ý quan trọng: Bậc tự do phải lớn hơn hoặc bằng 1. Nếu nhập số nhỏ hơn 1, hàm trả về lỗi #NUM! ngay lập tức.

Bước 4: Nhập công thức và xử lý lỗi

Quay lại ví dụ kiểm định điểm thi. Đã có t = 1.936 và df = 14. Công thức trong Excel:

=T.DIST.RT(1.936, 14)

Kết quả: 0.0367

Con số này là p-value đuôi bên phải. Với mức ý nghĩa 0.05, kết luận bác bỏ giả thuyết H₀ vì 0.0367 < 0.05. Điểm trung bình lớp này thực sự cao hơn 70.

Xử lý lỗi thường gặp:

Lỗi #VALUE! xuất hiện khi:

Tham số x là text: =T.DIST.RT("hai", 10) sai
Tham số deg_freedom là text: =T.DIST.RT(2, "mười") sai

Lỗi #NUM! xuất hiện khi:

Bậc tự do nhỏ hơn 1: =T.DIST.RT(2, 0) hoặc =T.DIST.RT(2, -5)

Nếu gặp lỗi, kiểm tra lại công thức tính t-statistic và bậc tự do. Hơn 80 phần trăm lỗi đến từ tính sai deg_freedom.

Bước 5: So sánh với giá trị tới hạn từ bảng tra

Hàm T.DIST.RT tính p-value trực tiếp. Bảng tra giá trị tới hạn cho giá trị t tương ứng với mức ý nghĩa cố định. Hai cách tiếp cận này tương đương nhưng hàm Excel linh hoạt hơn.

Phương pháp bảng tra:

Tra df = 14, α = 0.05 một phía
Tìm được t tới hạn = 1.761
So sánh: t tính (1.936) > t tới hạn (1.761)
Kết luận: Bác bỏ H₀

XEM THÊM: MAXA vs MAX: Sự Khác Biệt Quan Trọng Với Dữ Liệu Logic

Phương pháp hàm Excel:

Tính p-value = 0.0367
So sánh: p-value (0.0367) < α (0.05)
Kết luận: Bác bỏ H₀

Kết quả giống nhau nhưng hàm cho thông tin chi tiết hơn. Thay vì chỉ biết “bác bỏ” hay “chấp nhận”, p-value cho thấy mức độ mạnh yếu của bằng chứng. P-value 0.001 mạnh hơn nhiều so với 0.045 dù cả hai đều dưới 0.05.

Thêm vào đó, bảng tra thường chỉ có các mức α cố định như 0.1, 0.05, 0.025, 0.01. Hàm tính được p-value cho bất kỳ giá trị t nào. Nếu muốn kiểm định ở mức α = 0.03, bảng tra không có nhưng hàm vẫn hoạt động bình thường.

Ứng dụng với kiểm định hai phía

Kiểm định hai phía kiểm tra xem trung bình khác không, không quan tâm lớn hơn hay nhỏ hơn. P-value hai phía bằng hai lần p-value một phía.

Công thức:

=2 * T.DIST.RT(ABS(t), df)

Hàm ABS lấy giá trị tuyệt đối vì kiểm định hai phía không phân biệt dấu. Với t = -1.936 hoặc t = 1.936, kết quả giống nhau.

Ví dụ: =2 * T.DIST.RT(ABS(1.936), 14) cho ra 0.0734. So với mức ý nghĩa 0.05, không bác bỏ H₀ ở kiểm định hai phía.

Hoặc dùng trực tiếp hàm T.DIST.2T cho kiểm định hai phía: =T.DIST.2T(1.936, 14) cũng cho 0.0734. Excel 2010 trở lên có cả hai hàm này.

Lưu ý về phiên bản Excel

Hàm T.DIST.RT xuất hiện từ Excel 2010. Các phiên bản trước dùng hàm TDIST với cú pháp:

=TDIST(x, deg_freedom, tails)

Tham số tails bằng 1 cho kiểm định một phía, bằng 2 cho hai phía. Hàm TDIST vẫn hoạt động ở các phiên bản mới để tương thích ngược.

So sánh:

=T.DIST.RT(2.5, 10) giống =TDIST(2.5, 10, 1)
=T.DIST.2T(2.5, 10) giống =TDIST(2.5, 10, 2)

Nếu cần chia sẻ file với người dùng Excel 2007 trở xuống, hãy dùng TDIST thay vì T.DIST.RT. Kết quả hoàn toàn giống nhau, chỉ khác cú pháp.

Kết hợp với các hàm thống kê khác

T.DIST.RT thường đi kèm hàm T.INV.2T hoặc T.INV để tính giá trị tới hạn ngược lại. Thay vì cho t và nhận p-value, các hàm này cho p-value và nhận t.

Ví dụ tìm t tới hạn:

=T.INV.2T(0.05, 14)

Kết quả: 2.145 – đây chính là giá trị trong bảng tra tại df = 14, α = 0.05 hai phía.

XEM THÊM: Cách Dùng Hàm LINEST Để Dự Đoán Doanh Số Tháng Tới Trong 5 Phút

Kết hợp ba hàm này xử lý mọi tình huống kiểm định t:

T.DIST.RT: Cho t, tính p-value một phía
T.DIST.2T: Cho t, tính p-value hai phía
T.INV hoặc T.INV.2T: Cho p-value, tính t tới hạn

Tôi thường tạo template Excel với cả ba hàm sẵn. Chỉ cần nhập dữ liệu mẫu, các công thức tự động tính t-statistic và p-value. Tiết kiệm 15 phút mỗi lần làm bài tập thống kê.

Tối ưu hiệu suất tính toán

Với một vài phép tính, tốc độ không quan trọng. Nhưng khi phân tích 1000 dòng dữ liệu, mỗi dòng cần một kiểm định riêng, hiệu suất trở nên cần thiết.

Mẹo tăng tốc:

Tính t-statistic trong cột riêng trước
Dùng fill down cho công thức T.DIST.RT
Tránh nested functions sâu quá 3 level

Ví dụ thay vì:

=T.DIST.RT((A2-B2)/(C2/SQRT(D2)), D2-1)

Nên tách thành:

Cell E2: =(A2-B2)/(C2/SQRT(D2))
Cell F2: =D2-1  
Cell G2: =T.DIST.RT(E2, F2)

File tính nhanh hơn 40 phần trăm với dataset lớn. Thêm vào đó, dễ debug khi có lỗi vì nhìn thấy giá trị từng bước.

Khi nào vẫn cần dùng bảng tra

Hàm Excel hoàn hảo cho tính toán nhưng bảng tra vẫn có vai trò trong giáo dục. Sinh viên học thống kê cần hiểu cấu trúc phân bố t trước khi dùng công cụ tự động.

Trong kỳ thi không cho phép máy tính, bảng tra là lựa chọn duy nhất. Một số giáo trình vẫn yêu cầu tra bảng thủ công để kiểm tra hiểu biết lý thuyết.

Tuy nhiên, với công việc thực tế và nghiên cứu, hàm T.DIST.RT nhanh hơn, chính xác hơn và linh hoạt hơn. Bảng tra chỉ cho các mức α chuẩn, trong khi hàm tính được bất kỳ giá trị nào. Sai số đọc bảng cũng không còn là vấn đề.

Các bước tóm tắt nhanh

Quy trình hoàn chỉnh cho kiểm định giả thuyết bằng T.DIST.RT:

Tính t-statistic từ dữ liệu mẫu theo công thức phù hợp
Xác định bậc tự do dựa trên loại kiểm định và kích thước mẫu
Nhập =T.DIST.RT(t_value, df) để có p-value một phía
Nhân 2 nếu cần p-value hai phía hoặc dùng T.DIST.2T
So sánh p-value với mức ý nghĩa α để kết luận

Mỗi bước mất khoảng 10-15 giây. Tổng thời gian dưới một phút so với 5-10 phút nếu tra bảng thủ công. Với 20 bài kiểm định một ngày, tiết kiệm được gần 2 giờ.

Hàm hoạt động trên mọi phiên bản Excel từ 2010, Excel Online, và cả Google Sheets với tên hàm giống hệt. File tạo trên máy tính mở được ngay trên điện thoại hay tablet mà không cần cài thêm gì.