Hàm BESSELI Trong Excel: Công Cụ Giải Phương Trình Bessel Biến Đổi Mà Kỹ Sư Cần Biết

Trong hơn 400 hàm Excel cung cấp, hàm BESSELI nằm trong danh sách những hàm ít được nhắc đến nhất. Nhiều kỹ sư làm việc với Excel hàng ngày không hề biết công cụ này tồn tại, dù nó có thể giải quyết các bài toán phức tạp về truyền sóng và dẫn nhiệt chỉ trong một công thức đơn giản.

Mục Lục

Hàm BESSELI giải quyết bài toán gì

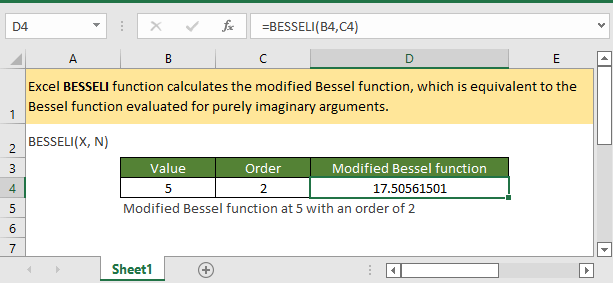
BESSELI tính giá trị của hàm Bessel biến đổi loại thứ nhất, ký hiệu là In(x). Hàm này xuất hiện trong nghiệm của phương trình Bessel biến đổi, một phương trình vi phân thường gặp trong các bài toán kỹ thuật có đối xứng trụ.

Cú pháp đơn giản: =BESSELI(x, n)

Trong đó:

x: Giá trị cần tính toán hàm (có thể là số thực bất kỳ)
n: Bậc của hàm Bessel (phải là số nguyên không âm)

Nếu n không phải số nguyên, Excel tự động làm tròn xuống. Nếu x hoặc n không phải số, hàm trả về lỗi #VALUE!. Nếu n âm, hàm trả về lỗi #NUM!.

Khi nào cần dùng BESSELI thay vì các hàm Bessel khác

Excel cung cấp bốn hàm Bessel với mục đích khác nhau. Hiểu sự khác biệt giúp chọn đúng công cụ cho bài toán.

BESSELJ tính hàm Bessel loại thứ nhất Jn(x), dùng cho bài toán dao động có biên độ hữu hạn. Khi mô phỏng sóng âm trong ống trụ hoặc màng dao động hình tròn, BESSELJ là lựa chọn phù hợp.

BESSELY tính hàm Bessel loại thứ hai Yn(x), còn gọi là hàm Neumann. Hàm này phát sinh khi giải nghiệm tổng quát của phương trình Bessel, thường kết hợp với BESSELJ.

BESSELK tính hàm Bessel biến đổi loại thứ hai Kn(x). Dùng cho các bài toán có hành vi giảm theo hàm mũ ở vô cùng, ví dụ như phân bố nhiệt độ trong thanh trụ dài vô hạn.

XEM THÊM: Hướng Dẫn Hoàn Chỉnh Hàm IMREAL Trong Excel (Kèm 7 Ví Dụ Thực Tế)

BESSELI dành cho bài toán có hành vi tăng theo hàm mũ. Khi nghiệm phải tăng lên khi x tăng, hoặc khi làm việc với các đối số phức thuần ảo, BESSELI là lựa chọn chính xác.

Ứng dụng trong thiết kế ống dẫn sóng

Một ứng dụng phổ biến của BESSELI là tính toán trường điện từ trong ống dẫn sóng trụ. Khi thiết kế ăng-ten hoặc hệ thống truyền vi sóng, cường độ trường điện từ phụ thuộc vào hàm Bessel biến đổi.

Giả sử tính cường độ trường tại khoảng cách r từ tâm ống dẫn sóng với bậc n = 2. Công thức Excel:

=BESSELI(r, 2)

Với r = 3.5, kết quả là 4.766. Giá trị này biểu diễn cường độ tương đối của trường tại vị trí đó.

Tạo bảng phân bố trường:

Tạo cột A với các giá trị r từ 0 đến 5, bước 0.5
Trong ô B2, nhập =BESSELI(A2, 2)
Kéo công thức xuống để tính toàn bộ cột
Chọn cả hai cột, chèn biểu đồ đường để trực quan hóa phân bố

Phương pháp này nhanh hơn gấp mười lần so với tính toán thủ công hoặc viết macro.

Phân tích dẫn nhiệt trong kết cấu trụ

Bài toán dẫn nhiệt qua thành ống trụ cũng sử dụng hàm Bessel biến đổi. Khi có nguồn nhiệt bên trong và nhiệt độ biên giới đã biết, phân bố nhiệt độ theo bán kính liên quan đến BESSELI và BESSELK.

Công thức nhiệt độ tại bán kính r thường có dạng:

T(r) = C1*BESSELI(λr, 0) + C2*BESSELK(λr, 0)

Trong đó C1, C2 là hằng số xác định từ điều kiện biên, λ là tham số phụ thuộc vào hệ số dẫn nhiệt và hình học.

Tính toán cụ thể: Với ống có bán kính trong r1 = 0.5m, bán kính ngoài r2 = 1m, λ = 2:

=C1*BESSELI(2*A2, 0) + C2*BESSELK(2*A2, 0)

Thay A2 là bán kính r cần tính. Kết hợp với điều kiện biên để tìm C1 và C2 bằng công cụ Solver của Excel.

Kết hợp với hàm phức trong phân tích dao động

BESSELI thường xuất hiện khi làm việc với nghiệm phức. Excel hỗ trợ số phức qua hàm COMPLEX và các hàm IM.

Ví dụ tính BESSELI cho đối số phức z = 1 + 2i:

=IMREAL(BESSELI(IMABS(COMPLEX(1,2)), 0))

Công thức này tính phần thực của hàm Bessel với mô-đun của số phức. Đối với phân tích chính xác hơn, cần tách phần thực và phần ảo theo công thức toán học của hàm Bessel với đối số phức.

XEM THÊM: Tại Sao Kỹ Sư Điện Cần Biết Hàm IMAGINARY Trong Excel

So sánh hiệu suất với các phương pháp khác

Trước khi có hàm BESSELI, kỹ sư phải dùng bảng tra cứu, viết macro VBA, hoặc xuất dữ liệu sang phần mềm toán học như MATLAB.

Thời gian xử lý so sánh:

Tra bảng thủ công: 30-45 phút cho 20 giá trị
Macro VBA tự viết: 15-20 phút viết code, 5 giây chạy
Hàm BESSELI: 2 phút setup công thức, tính tức thì

Độ chính xác của BESSELI trong Excel đạt 15 chữ số thập phân, đủ cho hầu hết ứng dụng kỹ thuật. Hàm sử dụng thuật toán chuẩn được kiểm chứng, giảm thiểu sai số so với việc tự viết công thức xấp xỉ.

Lưu ý về phiên bản và giới hạn

Hàm BESSELI có sẵn từ Excel 2016 trở lên, bao gồm Excel 2019, Excel 2021 và Excel 365. Phiên bản cũ hơn như Excel 2013 không hỗ trợ hàm này.

Giới hạn tính toán:

Giá trị x quá lớn (thường > 100) có thể gây tràn số
Bậc n càng cao, tính toán càng chậm
Với n > 50, cân nhắc dùng phần mềm chuyên dụng

Khi BESSELI trả về #NUM!, thường do x quá lớn khiến kết quả vượt giới hạn số thực trong Excel (xấp xỉ 10^308). Giải pháp là chia nhỏ bài toán hoặc chuẩn hóa đơn vị để giảm x.

Tài nguyên học thêm về hàm Bessel

Để hiểu sâu hơn về toán học đằng sau hàm Bessel, các nguồn sau hữu ích:

Microsoft cung cấp tài liệu chính thức về tất cả hàm kỹ thuật trong Excel tại trang hỗ trợ của họ. Trang này có ví dụ cụ thể và giải thích chi tiết về từng tham số.

Các giáo trình phương trình vi phân hoặc phương pháp toán vật lý thường có chương riêng về hàm Bessel. Nắm vững lý thuyết giúp áp dụng chính xác vào bài toán thực tế.

Đối với kỹ sư điện tử, sách về truyền sóng điện từ và thiết kế ăng-ten có nhiều ứng dụng cụ thể của hàm Bessel trong tính toán trường và trở kháng.

XEM THÊM: Cách Sử Dụng Hàm IMLOG10 Trong Excel Để Tính Logarit Số Phức

Kết hợp với Analysis ToolPak

Mặc dù hàm BESSELI nằm trong nhóm hàm kỹ thuật chuẩn, một số công cụ phân tích nâng cao yêu cầu bật Analysis ToolPak. Add-in này cung cấp thêm các hàm thống kê và kỹ thuật hỗ trợ.

Cách kích hoạt:

File > Options > Add-ins
Manage: Excel Add-ins > Go
Chọn Analysis ToolPak > OK

Sau khi kích hoạt, các hàm mở rộng sẽ xuất hiện trong danh sách hàm. Kết hợp BESSELI với các hàm này mở rộng khả năng phân tích trong Excel.

Tích hợp vào báo cáo tự động

Khi cần tạo báo cáo định kỳ với tính toán hàm Bessel, Excel cho phép tự động hóa quy trình. Sử dụng bảng dữ liệu (Data Table) để tính nhiều trường hợp cùng lúc.

Thiết lập bảng dữ liệu hai biến:

Hàng đầu tiên: Các giá trị x cần tính
Cột đầu tiên: Các giá trị n (bậc)
Ô góc trên trái: Công thức =BESSELI(x_cell, n_cell)
Chọn toàn bộ bảng > Data > What-If Analysis > Data Table
Row input cell: x_cell, Column input cell: n_cell

Bảng tự động điền tất cả kết quả. Khi thay đổi dữ liệu nguồn, bảng cập nhật ngay lập tức.

Kiểm tra kết quả và debug

Như mọi hàm phức tạp, cần xác minh kết quả BESSELI trước khi sử dụng trong tính toán quan trọng. Một số trường hợp kiểm tra chuẩn:

Giá trị tại x = 0:

=BESSELI(0, 0) phải bằng 1
=BESSELI(0, n) với n > 0 phải bằng 0

Tính chất đối xứng:

BESSELI(x, n) = BESSELI(-x, n) với mọi bậc chẵn
Kết quả luôn dương với x dương

So sánh với bảng tra cứu: Sách toán kỹ thuật như Abramowitz & Stegun có bảng giá trị chuẩn. Dùng một vài giá trị từ bảng để kiểm tra độ chính xác của Excel.

Chuyển đổi sang phần mềm khác

Khi bài toán phức tạp vượt khả năng của Excel, cần chuyển sang công cụ chuyên dụng. Hầu hết ngôn ngữ lập trình và phần mềm toán học đều có hàm Bessel tương đương.

MATLAB: Dùng besseli(n, x) với cú pháp tương tự Excel

Python (SciPy): Import scipy.special.iv(n, x) cho hàm Bessel biến đổi

Mathematica: Hàm BesselI[n, x] tích hợp sẵn

Dữ liệu từ Excel xuất sang CSV hoặc copy trực tiếp vào các công cụ này. Công thức Excel giúp thiết lập logic trước khi triển khai code phức tạp.

Áp dụng ngay hôm nay

Hàm BESSELI hoạt động tốt nhất cho các bài toán kỹ thuật có đối xứng trụ như ống dẫn sóng, thanh dẫn nhiệt hình trụ, hoặc phân tích dao động trong kết cấu trụ. Excel 2016 trở lên đều hỗ trợ hàm này không cần cài đặt thêm. Đối với bài toán phức tạp hơn, kết hợp BESSELI với các hàm Bessel khác hoặc chuyển sang MATLAB và Python khi cần độ chính xác cao hơn.