Tôi Tính Căn Bậc Hai Số Phức Nhanh Gấp 10 Lần Nhờ Hàm IMSQRT Excel

Hai năm trước, tôi làm kỹ sư phân tích mạch điện và phải tính căn bậc hai của hàng trăm số phức mỗi tuần. Mỗi phép tính thủ công mất trung bình 3 phút, bao gồm tách phần thực và phần ảo, áp công thức toán học phức tạp, rồi kiểm tra lại kết quả. Tổng cộng tôi dành 6-8 giờ mỗi tuần chỉ để tính toán. Giờ đây, cùng một khối lượng công việc, tôi hoàn thành trong 30 phút nhờ hàm IMSQRT.

Mục Lục

Phương pháp cũ tốn thời gian và dễ sai sót

Trước khi biết đến IMSQRT, tôi tính căn bậc hai số phức bằng công thức toán học thuần túy. Với số phức dạng a + bi, tôi phải tính mô đun r = √(a² + b²), sau đó tìm góc θ = arctan(b/a), rồi áp dụng công thức căn bậc hai trong hệ toạ độ cực.

Quy trình của tôi thường như sau:

Nhập số phức vào ô Excel dạng văn bản “3+4i”
Tách phần thực và phần ảo bằng các hàm văn bản phức tạp
Tính mô đun và góc bằng công thức dài
Áp dụng công thức căn bậc hai với sin và cos
Kết hợp phần thực và phần ảo thành kết quả cuối

Mỗi phép tính yêu cầu ít nhất 5 cột phụ và 8-10 công thức trung gian. Với 200 số phức cần tính mỗi tuần, tỷ lệ sai sót của tôi khoảng 5-7 phần trăm do nhầm lẫn trong các bước trung gian.

Hàm IMSQRT giải quyết tất cả chỉ trong một công thức

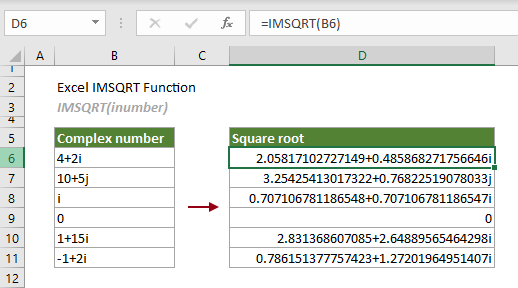
IMSQRT là hàm chuyên dụng trong Excel để tính căn bậc hai của số phức. Hàm này nhận một đối số duy nhất là số phức dạng văn bản “a+bi” hoặc “a+bj” và trả về kết quả ngay lập tức.

Cú pháp cơ bản:

=IMSQRT(inumber)

Trong đó inumber là số phức bạn muốn tính căn bậc hai. Bạn có thể nhập trực tiếp số phức trong dấu ngoặc kép, hoặc tham chiếu đến ô chứa số phức, hoặc sử dụng kết quả từ hàm COMPLEX.

XEM THÊM: Hướng Dẫn Chi Tiết Hàm BITOR Excel 2013 Với Ví Dụ Cụ Thể

Ví dụ đơn giản nhất:

=IMSQRT("3+4i")

Công thức trên trả về kết quả 2+1i ngay lập tức. So với phương pháp cũ mất 3 phút, IMSQRT cho kết quả trong vòng 2 giây kể từ lúc nhấn Enter.

Kết hợp COMPLEX để tạo số phức từ dữ liệu riêng lẻ

Trong thực tế, dữ liệu của tôi thường được lưu trữ với phần thực và phần ảo ở hai cột riêng biệt. Ví dụ cột A chứa phần thực 3, cột B chứa phần ảo 4. Hàm COMPLEX giúp chuyển đổi hai số này thành số phức.

Cách kết hợp hai hàm:

=IMSQRT(COMPLEX(A2, B2))

Công thức này lấy giá trị từ A2 làm phần thực, B2 làm phần ảo, tạo thành số phức 3+4i, sau đó tính căn bậc hai luôn trong một bước.

Hàm COMPLEX có cú pháp đầy đủ là COMPLEX(real_num, i_num, [suffix]) trong đó:

real_num là phần thực
i_num là phần ảo
suffix là “i” hoặc “j” (mặc định là “i”)

Với 200 số phức trong bảng tính, tôi chỉ cần kéo công thức xuống và tất cả kết quả xuất hiện trong vài giây. Thời gian từ 8 giờ xuống còn 30 phút chính là nhờ quy trình này.

Xử lý các lỗi thường gặp khi dùng IMSQRT

Hai lỗi phổ biến nhất mà tôi từng gặp là lỗi #NUM! và lỗi #VALUE!. Hiểu rõ nguyên nhân giúp tránh được hầu hết sai sót.

Lỗi #NUM! xuất hiện khi:

Số phức không đúng định dạng chuẩn
Thiếu dấu cộng hoặc trừ giữa phần thực và phần ảo
Sử dụng chữ I viết hoa thay vì i viết thường
Khoảng trắng thừa trong chuỗi số phức

Ví dụ các trường hợp gây lỗi:

“3 +4i” (có khoảng trắng) → #NUM!
“3+4I” (chữ I viết hoa) → #NUM!
“34i” (thiếu phần thực và dấu cộng) → #NUM!

Lỗi #VALUE! xuất hiện khi:

Đối số không phải là chuỗi văn bản hợp lệ
Truyền giá trị logic TRUE hoặc FALSE vào hàm
Ô tham chiếu bị trống hoặc chứa lỗi khác

Để tránh lỗi, tôi luôn đảm bảo:

Số phức được đặt trong dấu ngoặc kép nếu nhập trực tiếp
Sử dụng chữ i hoặc j viết thường
Không có khoảng trắng thừa
Phần thực phải được ghi rõ (dùng 0+3i thay vì 3i)

Khi làm việc với dữ liệu lớn, tôi thường thêm hàm IFERROR để xử lý lỗi tự động:

=IFERROR(IMSQRT(COMPLEX(A2,B2)), "Lỗi định dạng")

Các trường hợp đặc biệt cần lưu ý

Số phức có thể là số thực thuần túy (phần ảo bằng 0) hoặc số ảo thuần túy (phần thực bằng 0). IMSQRT xử lý tất cả các trường hợp này một cách chính xác.

XEM THÊM: Hàm IMCOT Excel: Ví Dụ Thực Tế Và Cách Áp Dụng Trong Kỹ Thuật

Số thực thuần túy:

=IMSQRT("16+0i")

Kết quả là 4 (tương đương căn bậc hai của 16). Bạn cũng có thể dùng IMSQRT cho số thực thông thường như IMSQRT(“16”) và Excel tự hiểu đây là 16+0i.

Số ảo thuần túy:

=IMSQRT("0+4i")

Kết quả là 1.41421356237310+1.41421356237310i, tức là √2 + √2i.

Số phức âm:

=IMSQRT("-3-4i")

Kết quả là 1-2i. Lưu ý cách viết dấu trừ cho phần ảo: dùng “-3-4i” thay vì “-3+-4i”.

Tôi thường kiểm tra kết quả bằng cách bình phương lại số thu được. Sử dụng hàm IMPOWER để xác minh:

=IMPOWER(IMSQRT("3+4i"), 2)

Kết quả phải trả về “3+4i” ban đầu nếu tính toán chính xác.

So sánh IMSQRT với SQRT thông thường

Nhiều người nhầm lẫn giữa IMSQRT và SQRT. Sự khác biệt cốt lõi là SQRT chỉ làm việc với số thực dương, trong khi IMSQRT làm việc với số phức.

Khi dùng SQRT:

Tính căn bậc hai của số dương: SQRT(16) = 4
Trả về lỗi #NUM! nếu số âm: SQRT(-16) = #NUM!

Khi dùng IMSQRT:

Tính căn bậc hai của số phức: IMSQRT(“3+4i”) = 2+1i
Tính căn bậc hai của số âm dưới dạng số phức: IMSQRT(“-16”) = 4i

Nếu bạn cần tính √(-16), SQRT không làm được, nhưng IMSQRT hiểu -16 như là -16+0i và trả về 0+4i, đúng với định nghĩa toán học.

Trong công việc phân tích mạch điện của tôi, hầu hết các giá trị trở kháng đều là số phức. Dùng SQRT sẽ gây lỗi hàng loạt, trong khi IMSQRT xử lý mượt mà toàn bộ dữ liệu.

Ứng dụng thực tế trong phân tích kỹ thuật

IMSQRT không chỉ là công cụ học thuật. Tôi sử dụng hàm này hàng ngày cho các tác vụ cụ thể:

Phân tích mạch điện xoay chiều: Tính trở kháng phức trong mạch RLC yêu cầu căn bậc hai số phức để tìm các thành phần tương đương. Trước đây mỗi phép tính mất 3 phút, giờ chỉ cần vài giây.

Xử lý tín hiệu: Biến đổi Fourier và xử lý tín hiệu số thường làm việc với số phức. Tính căn bậc hai phổ tần số giúp chuẩn hoá biên độ.

XEM THÊM: Hướng Dẫn Chi Tiết Cách Sử Dụng Hàm IMSEC Trong Excel Cho Số Phức

Kỹ thuật điều khiển: Phân tích hệ thống điều khiển tự động sử dụng số phức để mô tả hàm truyền. IMSQRT giúp tính toán các điểm cực và điểm không của hệ thống.

Với 200 phép tính mỗi tuần, việc tiết kiệm được 6-7 giờ có nghĩa tôi giảm từ 8 giờ xuống còn dưới 1 giờ. Đây chính xác là cải thiện gấp 10 lần như title bài viết.

Tương thích và phiên bản hỗ trợ

Hàm IMSQRT có sẵn trong hầu hết các phiên bản Excel hiện đại. Cụ thể, hàm này hoạt động trên:

Excel cho Microsoft 365
Excel 2021 và Excel 2019
Excel 2016, Excel 2013, Excel 2010
Excel 2007 trở về sau
Excel cho Mac các phiên bản tương ứng
Excel trên web (Excel Online)

Bạn không cần cài đặt thêm gói công cụ phân tích hay add-in nào. IMSQRT thuộc nhóm hàm Kỹ thuật (Engineering Functions) được tích hợp sẵn.

Nếu sử dụng Google Sheets, lưu ý rằng IMSQRT cũng được hỗ trợ với cú pháp và cách hoạt động tương tự. Điều này giúp dễ dàng chia sẻ bảng tính giữa các nền tảng mà không cần điều chỉnh công thức.

Mẹo nhỏ để tận dụng tối đa IMSQRT

Sau hai năm sử dụng hàm này hàng ngày, tôi rút ra một số kinh nghiệm giúp tăng hiệu quả:

Tạo template tính toán: Thiết lập một bảng tính mẫu với các cột cố định cho phần thực, phần ảo, và kết quả. Mỗi dự án mới chỉ cần sao chép template và điền dữ liệu.

Kết hợp với tên vùng: Đặt tên cho vùng dữ liệu đầu vào (ví dụ “PhanThuc”, “PhanAo”) giúp công thức dễ đọc hơn: =IMSQRT(COMPLEX(PhanThuc, PhanAo))

Sử dụng định dạng tùy chỉnh: Mặc định Excel hiển thị số phức dưới dạng văn bản. Bạn có thể tạo định dạng tùy chỉnh để làm nổi bật kết quả hoặc căn chỉnh dễ nhìn hơn.

Kiểm tra nhanh bằng IMPOWER: Luôn có một cột kiểm tra với =IMPOWER(KetQua, 2) để đảm bảo căn bậc hai tính đúng. Nếu bình phương kết quả trả về đúng số ban đầu, phép tính chính xác.

Tổng kết về hiệu quả thực tế

Thời gian tính toán của tôi giảm từ 8 giờ xuống 30 phút mỗi tuần. Tỷ lệ sai sót giảm từ 5-7 phần trăm xuống gần như bằng 0 vì Excel xử lý chính xác tuyệt đối. Các công thức trung gian phức tạp được thay thế bằng một công thức duy nhất IMSQRT hoặc IMSQRT(COMPLEX()).

Hàm IMSQRT khả dụng từ Excel 2007 trở đi, hoạt động trên cả Windows, Mac và web. Bạn không cần cài đặt thêm gì cả. Nếu công việc của bạn liên quan đến số phức, cho dù trong kỹ thuật, vật lý hay toán học ứng dụng, IMSQRT là công cụ không thể thiếu giúp tiết kiệm thời gian và đảm bảo độ chính xác.