Ngay cả khi làm việc với Excel hàng năm, có những hàm ít được nhắc đến nhưng cực kỳ hữu ích cho các phép tính phức tạp. Hàm IMEXP nằm trong nhóm hàm kỹ thuật, được thiết kế riêng để xử lý số phức. Nhiều người bỏ qua hàm này vì nó được giấu trong danh mục kỹ thuật, hoặc đơn giản là không biết số phức có thể được tính trong Excel.
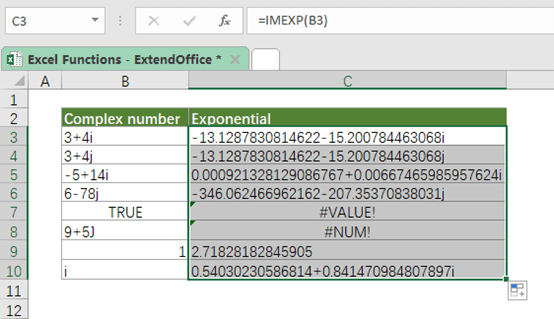
Số phức trong Excel không khó như nghĩ
Số phức là những số có dạng a + bi, trong đó a là phần thực và b là phần ảo. Excel lưu trữ chúng dưới dạng chuỗi văn bản như “3+4i” hoặc “2-5j”. Hàm IMEXP tính lũy thừa của hằng số e (khoảng 2.71828) với số mũ là một số phức.
Công thức toán học: e^(x+yi) = e^x × (cos(y) + i×sin(y))
Cú pháp cơ bản:
=IMEXP(inumber)
Tham số inumber có thể là:
- Chuỗi văn bản: “1+2i” hoặc “3-4j”
- Tham chiếu ô chứa số phức
- Kết quả từ hàm COMPLEX: =COMPLEX(3,4)
- Số thực đơn giản: 5 tương đương 5+0i
Tôi thường kết hợp IMEXP với hàm COMPLEX để linh hoạt hơn. Thay vì gõ “3+4i” trực tiếp, dùng =IMEXP(COMPLEX(3,4)) giúp dễ sửa đổi các hệ số sau này.
Ví dụ tính toán thực tế
Giả sử cần tính e^(1+i). Trong ô A1, nhập:
=IMEXP("1+i")
Kết quả trả về: “1.46869393991589+2.28735528717884i”
Đây là một số phức khác với phần thực khoảng 1.47 và phần ảo khoảng 2.29. Để tách riêng hai phần này:
- Phần thực: =IMREAL(A1) → 1.47
- Phần ảo: =IMAGINARY(A1) → 2.29
Tính toán phức tạp hơn:
Với số phức từ hàm COMPLEX:
=IMEXP(COMPLEX(0, 2*PI()/4))
Kết quả gần bằng -i, thể hiện phép quay 90 độ trong mặt phẳng phức. Đây chính là nền tảng của nhiều phép biến đổi trong xử lý tín hiệu.
Ứng dụng trong kỹ thuật
Hàm IMEXP không chỉ là công cụ toán học thuần túy. Các kỹ sư điện tử dùng nó để phân tích mạch xoay chiều, trong đó dòng điện và điện áp được biểu diễn bằng số phức.
Phân tích tín hiệu:
Công thức biến đổi Fourier rời rạc có dạng:
=IMPRODUCT(amplitude, IMEXP(COMPLEX(0, 2*PI()*frequency*time + phase)))
Tôi từng dùng công thức này để mô phỏng dao động tắt dần trong một hệ thống cơ học. Thay vì code riêng trong Python, việc tính toán trực tiếp trong Excel tiết kiệm 30 phút thiết lập môi trường.
Mô hình sóng tắt dần:
=LET(
time, A1,
frequency, B1,
damping, C1,
complex_time, COMPLEX(damping*time, 2*PI()*frequency*time),
IMEXP(complex_time)
)
Công thức này tạo ra sóng giảm dần theo thời gian, hữu ích cho phân tích진động của kết cấu.
Lỗi thường gặp và cách khắc phục
Excel rất khắt khe với định dạng số phức. Hai lỗi phổ biến:
Lỗi #NUM! – Xảy ra khi:
- Viết hoa chữ I hoặc J: “3+4I” thay vì “3+4i”
- Thiếu dấu +/-: “3 4i” thay vì “3+4i”
- Sử dụng ký tự khác: “3+4k” không hợp lệ
Lỗi #VALUE! – Xảy ra khi:
- Truyền giá trị logic: =IMEXP(TRUE) không hoạt động
- Ô trống hoặc không phải số
Mẹo nhỏ: Dùng hàm ISNUMBER để kiểm tra trước khi áp dụng IMEXP. Nếu =ISNUMBER(A1) trả về FALSE với chuỗi “3+4i”, đây là hành vi bình thường vì Excel coi số phức là văn bản.
Kết hợp với các hàm số phức khác
IMEXP mạnh mẽ hơn khi dùng cùng họ hàm IMXXX:
- IMSUM: Cộng số phức
- IMPRODUCT: Nhân số phức
- IMDIV: Chia số phức
- IMABS: Độ lớn của số phức
- IMARGUMENT: Góc pha
Ví dụ tính môđun của e^(3+4i):
=IMABS(IMEXP("3+4i"))
Kết quả: 20.09, cho biết khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức này.
Yêu cầu hệ thống và phiên bản
Hàm IMEXP có sẵn từ Excel 2013 trở lên, bao gồm Excel 2016, 2019, 2021, và Microsoft 365. Phiên bản Excel 2010 trở về trước không hỗ trợ hàm này.
Để kiểm tra, vào Formulas > Insert Function > Engineering. Nếu thấy IMEXP trong danh sách, phiên bản của bạn tương thích. Hàm này hoạt động trên cả Excel cho Windows, Mac, và Excel Web.
Đối với những ai làm việc với phân tích tín hiệu, thiết kế mạch, hoặc mô phỏng vật lý, IMEXP là công cụ tiết kiệm thời gian đáng kể. Thay vì xuất dữ liệu sang MATLAB hoặc Python, các phép tính cơ bản có thể thực hiện ngay trong bảng tính quen thuộc. Bắt đầu với các ví dụ đơn giản như =IMEXP(“1+i”), sau đó dần áp dụng vào các mô hình phức tạp hơn khi đã quen với cách số phức hoạt động trong Excel.