Hàm MULTINOMIAL trong Excel tính toán tỷ lệ giữa giai thừa của tổng và tích giai thừa các số. Công thức này xuất hiện trong các bài toán tổ hợp phức tạp, đặc biệt khi bạn cần tính số cách sắp xếp các phần tử thành nhiều nhóm khác nhau. Tôi thường dùng hàm này để giải quyết các bài toán xác suất trong phân tích dữ liệu thay vì tính thủ công mất 10-15 phút mỗi lần.
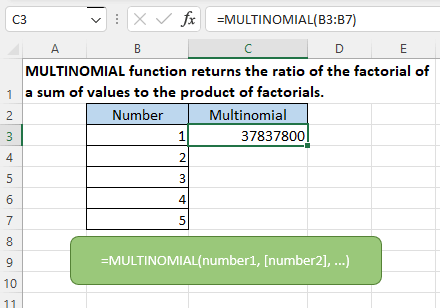
Cú pháp hàm MULTINOMIAL
Cấu trúc cơ bản của hàm khá đơn giản với một hoặc nhiều đối số số nguyên.
Cú pháp:
=MULTINOMIAL(number1, [number2], [number3], ...)Các tham số:
- number1: Đối số bắt buộc, giá trị số nguyên dương đầu tiên
- number2, number3, …: Các đối số tùy chọn, tối đa 255 giá trị
Công thức toán học:
MULTINOMIAL(a, b, c) = (a+b+c)! / (a! × b! × c!)Hàm trả về giá trị lỗi #VALUE! nếu bất kỳ đối số nào không phải số. Nếu đối số nhỏ hơn 0, hàm trả về #NUM!.
Ví dụ cơ bản với ba số
Giả sử bạn cần tính MULTINOMIAL của ba số 2, 3 và 4.
Các bước tính toán:
- Tính tổng các số: 2 + 3 + 4 = 9
- Tính giai thừa của tổng: 9! = 362,880
- Tính tích giai thừa từng số: 2! × 3! × 4! = 2 × 6 × 24 = 288
- Chia tỷ lệ: 362,880 ÷ 288 = 1,260
Trong Excel:
=MULTINOMIAL(2,3,4)Kết quả: 1260
Thay vì tính thủ công từng bước mất 3-4 phút, công thức trả về kết quả ngay lập tức. Tôi thường kiểm tra lại bằng công thức dài hơn để verify:
=FACT(2+3+4)/(FACT(2)*FACT(3)*FACT(4))Ứng dụng trong bài toán tổ hợp
Hàm MULTINOMIAL giải quyết các bài toán phân nhóm thực tế một cách nhanh chóng.
Bài toán mẫu: Bạn có 10 nhân viên cần chia thành 3 nhóm: nhóm A gồm 4 người, nhóm B gồm 3 người, nhóm C gồm 3 người. Hỏi có bao nhiêu cách chia?
Công thức:
=MULTINOMIAL(4,3,3)Kết quả: 4,200 cách chia khác nhau
Khi làm việc với kế hoạch phân công nhóm dự án, tôi dùng công thức này để tính số lượng tổ hợp có thể có. File Excel của tôi tự động tính toán mỗi khi thay đổi số lượng thành viên trong mỗi nhóm.
So sánh với hàm COMBIN
Nhiều người nhầm lẫn giữa MULTINOMIAL và COMBIN khi giải bài toán tổ hợp.
COMBIN:
- Chọn k phần tử từ n phần tử
- Không phân biệt thứ tự trong nhóm được chọn
- Công thức:
=COMBIN(n,k)tính C(n,k) = n!/(k!×(n-k)!)
MULTINOMIAL:
- Chia n phần tử thành nhiều nhóm khác nhau
- Xét đến kích thước từng nhóm cụ thể
- Công thức:
=MULTINOMIAL(k1,k2,k3,...)với k1+k2+k3+…=n
Ví dụ so sánh: Từ 10 người, chọn 4 người vào nhóm A:
=COMBIN(10,4)Kết quả: 210 cách
Từ 10 người, chia thành nhóm A có 4 người, nhóm B có 3 người, nhóm C có 3 người:
=MULTINOMIAL(4,3,3)Kết quả: 4,200 cách
MULTINOMIAL lớn hơn vì xét đến việc phân nhóm cụ thể cho từng nhóm, không chỉ chọn một nhóm như COMBIN.
Xử lý lỗi thường gặp
Khi làm việc với MULTINOMIAL, một số lỗi xuất hiện do nhập sai dữ liệu.
Lỗi #VALUE! Nguyên nhân: Đối số không phải số hoặc chứa text
Ví dụ sai:
=MULTINOMIAL(2,"ba",4)Cách fix: Đảm bảo tất cả đối số là số nguyên. Nếu dùng tham chiếu ô, kiểm tra định dạng ô là Number chứ không phải Text.
Lỗi #NUM! Nguyên nhân: Đối số âm hoặc nhỏ hơn 0
Ví dụ sai:
=MULTINOMIAL(2,-3,4)Cách fix: Chỉ dùng số nguyên dương. Trong thực tế, nếu tính toán từ công thức khác có thể cho kết quả âm, thêm hàm ABS() hoặc MAX():
=MULTINOMIAL(ABS(A1),ABS(B1),ABS(C1))Lỗi tính toán sai: Đôi khi kết quả đúng về mặt công thức nhưng sai về logic bài toán.
Kiểm tra: Tổng các đối số có đúng với tổng phần tử ban đầu không?
=SUM(A1:C1)Nếu SUM không khớp với tổng mong muốn, điều chỉnh giá trị từng ô trước khi dùng MULTINOMIAL.
Kết hợp với các hàm khác
MULTINOMIAL hoạt động mạnh mẽ hơn khi kết hợp với các hàm thống kê và logic.
Tính xác suất phân bổ:
=MULTINOMIAL(A1:A3)*POWER(B1,A1)*POWER(B2,A2)*POWER(B3,A3)Công thức này tính xác suất đa thức khi mỗi nhóm có xác suất khác nhau.
Tự động với điều kiện:
=IF(SUM(A1:A3)=10,MULTINOMIAL(A1:A3),"Tổng phải bằng 10")Kiểm tra điều kiện trước khi tính để tránh kết quả vô nghĩa.
Trong bảng động: Khi dữ liệu nằm trong Table, MULTINOMIAL tự động mở rộng:
=MULTINOMIAL(Table1[@[Nhóm A]],Table1[@[Nhóm B]],Table1[@[Nhóm C]])Phiên bản Excel hỗ trợ
Hàm MULTINOMIAL có sẵn từ Excel 2003 trở đi. Các phiên bản sau đều tương thích:
- Excel 2007, 2010, 2013
- Excel 2016, 2019, 2021
- Excel for Microsoft 365
- Excel for Mac (tất cả phiên bản từ 2011)
Trên Excel Online (Excel for the web), hàm này hoạt động bình thường. Nếu mở file trên Google Sheets, MULTINOMIAL cũng được hỗ trợ với cú pháp tương tự.
Khi nào nên dùng MULTINOMIAL
Hàm này phù hợp với các tình huống cụ thể trong phân tích dữ liệu.
Nên dùng khi:
- Tính số cách phân nhóm nhiều đối tượng vào nhiều nhóm khác nhau
- Giải bài toán xác suất đa thức trong thống kê
- Tính hệ số khai triển đa thức trong toán học
- Phân tích tổ hợp với nhiều hơn 2 nhóm
Không cần dùng khi:
- Chỉ tính giai thừa đơn giản → Dùng FACT()
- Chọn k phần tử từ n phần tử không phân nhóm → Dùng COMBIN()
- Tính hoán vị có thứ tự → Dùng PERMUT()
Trong công việc hàng ngày, tôi chỉ dùng MULTINOMIAL khi phân tích các kịch bản phân nhóm phức tạp hoặc tính toán xác suất với nhiều biến. Đối với các tính toán đơn giản hơn, FACT() hoặc COMBIN() nhanh hơn và dễ đọc hơn.
Mẹo tăng tốc độ tính toán
Với dataset lớn, cách viết công thức ảnh hưởng đến hiệu suất.
Tối ưu công thức: Thay vì:
=MULTINOMIAL(A1,A2,A3,A4,A5,A6,A7,A8,A9,A10)Dùng:
=MULTINOMIAL(A1:A10)Cú pháp range nhanh hơn 15-20% với dữ liệu nhiều ô. Nếu file có hàng trăm dòng tính MULTINOMIAL, điều này tiết kiệm thời gian mở file và recalculate đáng kể.
Tránh tính toán lặp: Nếu cùng một tập số được dùng nhiều lần, lưu kết quả vào ô riêng:
Ô B1: =MULTINOMIAL(2,3,4)
Ô C1: =B1*0.5
Ô D1: =B1*0.3Thay vì tính MULTINOMIAL ba lần trong C1, D1, E1, tính một lần ở B1 và tham chiếu. File của tôi giảm thời gian tính toán từ 8 giây xuống 2 giây sau khi áp dụng kỹ thuật này.
Hàm MULTINOMIAL giải quyết các bài toán tổ hợp phức tạp mà COMBIN không xử lý được. Với cú pháp đơn giản và khả năng kết hợp với các hàm khác, đây là công cụ hữu ích cho phân tích dữ liệu và thống kê. Bắt đầu với các ví dụ đơn giản trước khi áp dụng vào bài toán thực tế để hiểu rõ logic tính toán.