Tôi mất 3 giờ đồng hồ debug một bảng tính toán kỹ thuật chỉ vì nhập góc 60 độ thẳng vào hàm COS. Kết quả trả về -0.95 thay vì 0.5 như mong đợi. Hóa ra Excel tính toán theo radian, không phải độ. Sau khi nghiên cứu kỹ, tôi phát hiện có đến 2 cách chuyển đổi mà hầu hết người dùng không hề biết.
Vấn đề cốt lõi với hàm COS
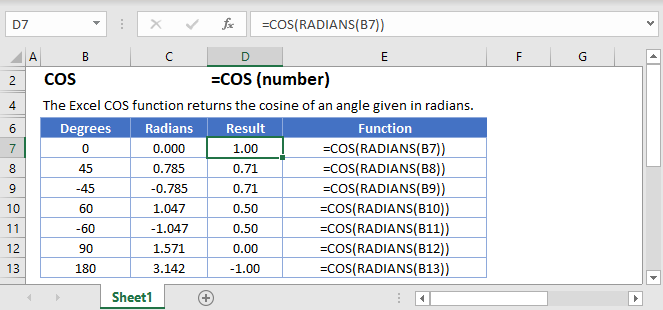
Hàm COS trong Excel chỉ chấp nhận góc tính bằng radian. Nếu góc của bạn đo bằng độ như thông thường, bạn phải chuyển đổi trước. Công thức cơ bản là =COS(góc_radian) nhưng đây chính là nơi 90% người dùng mắc sai lầm.
Ví dụ sai phổ biến: Nhập =COS(60) khi muốn tính cos của 60 độ sẽ cho kết quả -0.95. Con số này hoàn toàn sai vì Excel hiểu 60 là 60 radian, không phải 60 độ.
Kết quả đúng: Cos của 60 độ phải là 0.5. Để có được con số này, bạn cần một trong hai phương pháp dưới đây.
Phương pháp 1: Hàm RADIANS chuyển đổi tự động
Đây là cách tôi dùng nhiều nhất vì dễ nhớ và logic rõ ràng.
Cú pháp: =COS(RADIANS(góc_độ))
Cách thực hiện:
- Chọn ô cần hiển thị kết quả
- Nhập công thức:
=COS(RADIANS(B2))- B2 chứa góc đo bằng độ, ví dụ 60
- Nhấn Enter
Ưu điểm vượt trội:
- Dễ đọc và hiểu ngay ý nghĩa: chuyển độ sang radian rồi tính cos
- Không cần nhớ công thức toán học phức tạp
- Hàm RADIANS có sẵn từ Excel 2007, tương thích hầu hết phiên bản
Ví dụ thực tế: Bảng tính của tôi có góc 30, 45, 60, 90 độ trong cột B. Tôi nhập =COS(RADIANS(B2)) vào ô C2, kéo công thức xuống. Kết quả:
- 30 độ → 0.866
- 45 độ → 0.707
- 60 độ → 0.5
- 90 độ → 0 (chính xác 6.12E-17 do sai số làm tròn)
Phương pháp 2: Nhân với PI()/180
Đây là phương pháp toán học thuần túy, hữu ích khi làm việc với công thức phức tạp.
Cú pháp: =COS(góc_độ*PI()/180)
Cách thực hiện:
- Chọn ô kết quả
- Nhập công thức:
=COS(B2*PI()/180)- B2 chứa góc độ
- Nhấn Enter
Ưu điểm đặc biệt:
- Không phụ thuộc vào hàm RADIANS (hữu ích với Excel cũ)
- Nhanh hơn một chút khi lồng trong công thức lớn
- Thể hiện rõ nguyên lý toán học: 1 độ = π/180 radian
Khi nào nên dùng: Tôi dùng phương pháp này khi kết hợp nhiều phép tính lượng giác. Ví dụ tính khoảng cách theo công thức: =B2*COS(C2*PI()/180)+D2*SIN(C2*PI()/180). Việc dùng *PI()/180 giúp công thức gọn hơn so với lồng nhiều hàm RADIANS.
So sánh hai phương pháp
Cả hai cách đều cho kết quả giống hệt nhau về mặt toán học. Sự khác biệt nằm ở khả năng đọc hiểu và bối cảnh sử dụng.
Dùng RADIANS khi:
- Làm việc với đồng nghiệp ít kinh nghiệm Excel
- Cần công thức dễ maintenance
- Có góc đo bằng độ từ nguồn bên ngoài
Dùng PI()/180 khi:
- Công thức đã có nhiều hàm lồng nhau
- Tối ưu độ dài công thức
- Làm việc với Excel 2003 trở xuống
Lỗi thường gặp và cách tránh:
Lỗi #NUM! xuất hiện nếu bạn vô tình nhập giá trị văn bản thay vì số. Kiểm tra ô đầu vào bằng hàm =ISNUMBER(B2) để chắc chắn.
Lỗi #VALUE! xảy ra khi ô tham chiếu trống hoặc chứa ký tự đặc biệt. Dùng hàm =IFERROR(COS(RADIANS(B2)),0) để xử lý các trường hợp này.
Thêm mẹo nâng cao: Hàm ACOS
Nếu bạn có giá trị cos và muốn tìm ngược lại góc, dùng hàm ACOS.
Cú pháp: =ACOS(giá_trị_cos)*180/PI()
Ví dụ: =ACOS(0.5)*180/PI() trả về 60 độ. Lưu ý giá trị đầu vào phải nằm trong khoảng -1 đến 1, nếu không Excel sẽ báo lỗi #NUM!.
Áp dụng ngay hôm nay
Hai phương pháp này hoạt động từ Excel 2007 trở lên, bao gồm cả Excel 365 và Excel Online. Bắt đầu với RADIANS nếu bạn mới làm quen, chuyển sang PI()/180 khi đã thành thạo và cần tối ưu công thức.
Điểm mấu chốt: Luôn nhớ chuyển đổi độ sang radian trước khi dùng hàm COS. Hai phương pháp trên giúp bạn tránh được 99% lỗi tính toán lượng giác trong Excel.