Tôi Dùng Sai Hàm ATAN Trong Excel Suốt 3 Năm Cho Đến Khi Khám Phá ATAN2

Trong 3 năm làm việc với dữ liệu tọa độ, tôi luôn dùng hàm ATAN để tính góc. Công thức của tôi là =ATAN(y/x), đơn giản và có vẻ hoạt động tốt. Cho đến một ngày, tôi nhận ra kết quả sai lệch hoàn toàn khi điểm nằm ở góc phần tư thứ hai và thứ ba. Công thức trả về cùng một góc cho hai điểm hoàn toàn đối diện nhau. Đó là lúc tôi phát hiện ATAN2 và nhận ra mình đã bỏ lỡ một hàm quan trọng suốt thời gian dài.

Vấn đề tôi gặp với hàm ATAN

Hàm ATAN chỉ nhận một đối số duy nhất là tỷ số y/x. Kết quả trả về nằm trong khoảng từ -π/2 đến π/2 radian, tương đương -90 độ đến 90 độ. Điều này có nghĩa ATAN chỉ phân biệt được góc phần tư thứ nhất và thứ tư.

Ví dụ cụ thể về sai lệch:

Điểm A có tọa độ (1, 1) và điểm B có tọa độ (-1, -1). Về mặt hình học, hai điểm này nằm hoàn toàn đối diện nhau qua gốc tọa độ, góc của chúng chênh lệch 180 độ. Nhưng khi tôi dùng =ATAN(1/1) cho điểm A và =ATAN(-1/-1) cho điểm B, cả hai đều trả về 0.785398 radian hay 45 độ.

Lý do là ATAN chỉ xét tỷ số y/x. Dù x và y có dấu gì, sau khi chia, tỷ số (-1)/(-1) vẫn bằng 1, giống hệt 1/1. Hàm không thể biết được dấu của x và y riêng lẻ, nên không thể xác định điểm nằm ở góc phần tư nào.

Tôi phải thêm nhiều hàm IF phức tạp để kiểm tra dấu của x và y, rồi cộng trừ π thủ công. Công thức dài dòng và dễ sai.

XEM THÊM: Tại sao hàm ACOS lại quan trọng đến vậy mà tôi mất cả tuần để hiểu rõ nó?

ATAN2 giải quyết hoàn toàn vấn đề

Hàm ATAN2 nhận hai đối số riêng biệt: tọa độ x và tọa độ y. Cú pháp là =ATAN2(x, y). Nhờ có cả hai giá trị, hàm xác định chính xác góc trong cả bốn góc phần tư. Kết quả trả về nằm trong khoảng từ -π đến π radian, tương đương -180 độ đến 180 độ.

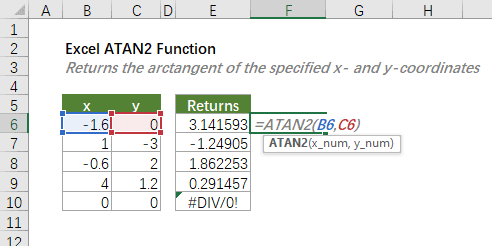
Quay lại ví dụ trên, khi tôi dùng =ATAN2(1, 1) cho điểm A, kết quả là 0.785398 radian hay 45 độ. Với điểm B, công thức =ATAN2(-1, -1) trả về -2.356194 radian hay -135 độ. Chênh lệch chính xác 180 độ như mong đợi.

Ưu điểm vượt trội:

ATAN2 không cần kiểm tra điều kiện. Hàm tự động xử lý mọi trường hợp dựa trên dấu của x và y. Kết quả dương thể hiện góc quay ngược chiều kim đồng hồ từ trục x, kết quả âm thể hiện góc quay cùng chiều kim đồng hồ.

Thậm chí khi x bằng 0, ATAN2 vẫn hoạt động bình thường. Trong khi ATAN(y/0) gây lỗi chia cho không, ATAN2(0, y) trả về đúng góc 90 độ hoặc -90 độ tùy dấu của y. Điều này đặc biệt hữu ích khi làm việc với dữ liệu thực tế có thể chứa các điểm thẳng đứng.

So sánh chi tiết ATAN và ATAN2

Để thấy rõ sự khác biệt, tôi tạo bảng tính với các điểm ở cả bốn góc phần tư:

Góc phần tư I (x dương, y dương):

Điểm (3, 3): ATAN(3/3) = 0.785 rad (45°), ATAN2(3, 3) = 0.785 rad (45°)
Cả hai hàm cho kết quả giống nhau

XEM THÊM: 2 Phương Pháp Tính Hàm COS Mà 90% Người Dùng Excel Không Biết

Góc phần tư II (x âm, y dương):

Điểm (-3, 3): ATAN(3/-3) = -0.785 rad (-45°), ATAN2(-3, 3) = 2.356 rad (135°)
ATAN sai hoàn toàn, ATAN2 đúng

Góc phần tư III (x âm, y âm):

Điểm (-3, -3): ATAN(-3/-3) = 0.785 rad (45°), ATAN2(-3, -3) = -2.356 rad (-135°)
ATAN lại cho kết quả 45° như góc phần tư I, ATAN2 chính xác

Góc phần tư IV (x dương, y âm):

Điểm (3, -3): ATAN(-3/3) = -0.785 rad (-45°), ATAN2(3, -3) = -0.785 rad (-45°)
Cả hai hàm cho kết quả giống nhau

Như vậy, ATAN chỉ làm việc đúng với góc phần tư I và IV. Còn ATAN2 xử lý chính xác cả bốn góc phần tư.

Cú pháp và ví dụ thực tế

Cú pháp chuẩn:

=ATAN2(x_num, y_num)

Trong đó:

x_num: Tọa độ trên trục hoành (trục x)
y_num: Tọa độ trên trục tung (trục y)

Lưu ý quan trọng: Thứ tự tham số là x trước, y sau. Một số ngôn ngữ lập trình khác như Python dùng thứ tự ngược lại, nên cần chú ý khi chuyển đổi công thức.

Ví dụ tính góc của vector:

Giả sử tôi có danh sách tọa độ các điểm trong ô A2:B10. Cột A chứa giá trị x, cột B chứa giá trị y. Để tính góc của mỗi điểm với trục x, tôi nhập công thức tại ô C2:

=ATAN2(A2, B2)

Kéo công thức xuống các ô phía dưới. Kết quả hiển thị bằng radian. Nếu cả x và y đều bằng 0, hàm trả về lỗi #DIV/0! vì không xác định được góc của điểm gốc tọa độ.

Xử lý lỗi:

XEM THÊM: Cách Dùng Hàm CEILING Để Làm Tròn Đến Bội Số Gần Nhất Trong Excel

Để tránh hiển thị lỗi khi gặp điểm (0,0), tôi bọc công thức trong hàm IFERROR:

=IFERROR(ATAN2(A2, B2), "Không xác định")

Chuyển đổi từ radian sang độ

Kết quả của ATAN2 luôn ở dạng radian. Để chuyển sang độ, có hai cách:

Cách 1: Dùng hàm DEGREES

=DEGREES(ATAN2(A2, B2))

Hàm DEGREES nhận giá trị radian và tự động chuyển sang độ. Đây là cách tôi thích nhất vì rõ ràng và dễ đọc.

Cách 2: Nhân với 180/PI()

=ATAN2(A2, B2) * 180/PI()

Cả hai cách cho kết quả giống hệt nhau. Ví dụ, với điểm (1, 1):

ATAN2(1, 1) = 0.785398 radian
DEGREES(ATAN2(1, 1)) = 45 độ
ATAN2(1, 1) * 180/PI() = 45 độ

Nếu cần làm tròn kết quả, kết hợp với hàm ROUND:

=ROUND(DEGREES(ATAN2(A2, B2)), 2)

Công thức này làm tròn đến 2 chữ số thập phân. Với điểm (2, 3), kết quả là 56.31 độ thay vì 56.309932474 độ.

Khi nào dùng ATAN2 thay vì ATAN

Sau khi so sánh kỹ, tôi rút ra quy tắc đơn giản: dùng ATAN2 trong hầu hết các trường hợp liên quan đến tọa độ. Chỉ dùng ATAN khi bạn chắc chắn chỉ làm việc với góc phần tư I và IV, hoặc khi bạn đã có sẵn tỷ số y/x và không quan tâm đến góc phần tư.

ATAN2 tương thích với Excel 2007 trở lên, bao gồm Excel 2010, 2013, 2016, 2019, 2021 và Excel 365. Hàm cũng hoạt động trên Excel for Mac. Nếu công thức của bạn đang dùng ATAN kèm nhiều hàm IF để điều chỉnh góc, hãy thay thế bằng ATAN2 ngay. Công thức ngắn hơn, chính xác hơn và dễ bảo trì hơn rất nhiều.