Hàm GEOMEAN Trong Excel: Khi Nào Dùng Thay Vì AVERAGE

Hầu hết mọi người dùng hàm AVERAGE để tính trung bình mọi thứ trong Excel, kể cả những trường hợp nó cho kết quả sai. Tôi từng tính tỷ lệ tăng trưởng hàng năm của danh mục đầu tư bằng AVERAGE và tự hỏi tại sao số liệu không khớp với thực tế. Hóa ra GEOMEAN mới là hàm đúng cho các phép tính liên quan đến phần trăm, tỷ lệ và sự tăng trưởng theo thời gian.

Mục Lục

AVERAGE Tính Gì Và GEOMEAN Tính Gì

AVERAGE cộng tất cả các số rồi chia cho số lượng phần tử. Với dãy số 10, 20, 30, kết quả là 20. Công thức toán học là tổng chia số lượng, còn gọi là trung bình cộng.

GEOMEAN lấy căn bậc n của tích các số. Với cùng dãy 10, 20, 30, kết quả là 18.17. Công thức là căn bậc ba của 10×20×30, còn gọi là trung bình nhân.

Cú pháp AVERAGE:

=AVERAGE(số1, [số2], ...)
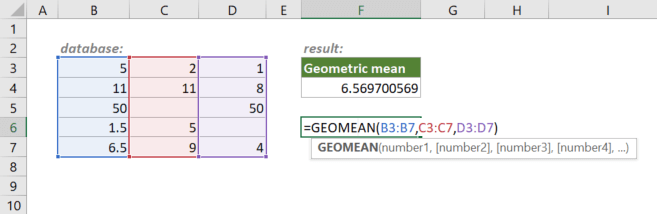
=AVERAGE(C2:C10)

Cú pháp GEOMEAN:

=GEOMEAN(số1, [số2], ...)
=GEOMEAN(C2:C10)

Cả hai hàm đều chấp nhận tối đa 255 đối số, có thể là số đơn lẻ, phạm vi ô hoặc kết hợp cả hai. GEOMEAN yêu cầu tất cả số phải dương, nếu có số âm hoặc số 0 sẽ trả về lỗi số NUM.

Tại Sao AVERAGE Sai Khi Tính Tỷ Lệ Tăng Trưởng

Giả sử bạn đầu tư 100 triệu. Năm đầu tăng 50 phần trăm lên 150 triệu. Năm hai giảm 50 phần trăm xuống 75 triệu. Dùng AVERAGE để tính tỷ lệ tăng trưởng trung bình sẽ cho kết quả 0 phần trăm, nhưng thực tế bạn mất 25 triệu.

Tính sai với AVERAGE:

Năm 1: +50%
Năm 2: -50%
AVERAGE: (50 + (-50)) / 2 = 0%
→ Kết luận sai: Không lời không lỗ

Tính đúng với GEOMEAN:

Năm 1: 150/100 = 1.5 (tăng trưởng 150%)
Năm 2: 75/150 = 0.5 (giảm còn 50%)
GEOMEAN(1.5, 0.5) = 0.866
→ Tỷ lệ tăng trưởng: -13.4% mỗi năm

Tôi từng báo cáo sai tỷ lệ tăng trưởng cho quản lý trong 4 tháng trước khi phát hiện công thức dùng AVERAGE. Chuyển sang GEOMEAN, số liệu khớp với kết quả thực tế ngay lập tức.

XEM THÊM: Hàm SKEW Trong Excel: Cách Phân Tích Độ Lệch Dữ Liệu Trong 5 Phút

Khi Nào Dùng AVERAGE

AVERAGE phù hợp khi các giá trị độc lập và cộng dồn. Điểm số, nhiệt độ, chiều cao, thời gian phản hồi đều nên dùng AVERAGE.

Ví dụ điểm trung bình học sinh:

Toán: 8
Lý: 7
Hóa: 9
AVERAGE(8,7,9) = 8.0

Mỗi môn học độc lập, điểm các môn cộng lại rồi chia đều. Đây là trường hợp chính xác cho AVERAGE.

Ví dụ thời gian phản hồi website:

Request 1: 120ms
Request 2: 150ms
Request 3: 100ms
AVERAGE(120,150,100) = 123.3ms

Đo lường hiệu suất trung bình dựa trên các lần đo độc lập. AVERAGE cho kết quả có ý nghĩa.

Quy tắc nhanh: Nếu bạn có thể cộng các giá trị lại và tổng có ý nghĩa, dùng AVERAGE. Nếu bạn phải nhân các giá trị hoặc chúng là tỷ lệ phần trăm, dùng GEOMEAN.

Khi Nào Dùng GEOMEAN

GEOMEAN bắt buộc cho ba trường hợp: tỷ lệ tăng trưởng, tỷ lệ phần trăm thay đổi và lãi suất kép. Bất kỳ tình huống nào giá trị mới phụ thuộc vào giá trị trước đó.

Trường hợp 1: Tỷ lệ tăng trưởng doanh thu

Công ty tăng doanh thu 20 phần trăm năm đầu, 30 phần trăm năm hai, 10 phần trăm năm ba.

Năm 1: 1.20 (tăng 20%)
Năm 2: 1.30 (tăng 30%)  
Năm 3: 1.10 (tăng 10%)
GEOMEAN(1.20, 1.30, 1.10) = 1.197
→ Tăng trưởng trung bình: 19.7% mỗi năm

Dùng AVERAGE cho ra 20 phần trăm, nhưng áp dụng ngược lại không khớp với doanh thu thực tế cuối cùng.

Trường hợp 2: Lãi suất đầu tư kép

Đầu tư 50 triệu với lãi suất thay đổi: năm một 15 phần trăm, năm hai 8 phần trăm, năm ba 12 phần trăm.

=50000000 * (1 + (GEOMEAN(1.15, 1.08, 1.12) - 1))^3

GEOMEAN tính lãi suất trung bình chính xác khi lãi được cộng dồn hàng năm.

Trường hợp 3: Hiệu suất so sánh giữa các khoảng thời gian

So sánh tốc độ tăng trưởng của hai sản phẩm qua 6 tháng với dữ liệu dao động mạnh.

Sản phẩm A: 1.5, 0.8, 1.2, 0.9, 1.4, 1.1
Sản phẩm B: 1.1, 1.1, 1.0, 1.2, 1.0, 1.1
GEOMEAN(A) = 1.11 → +11% trung bình
GEOMEAN(B) = 1.08 → +8% trung bình

GEOMEAN cân bằng ảnh hưởng của các đỉnh và đáy cực đoan. Sản phẩm A có biến động cao hơn nhưng tăng trưởng thực tế mạnh hơn.

XEM THÊM: Hàm FORECAST.LINEAR Giúp Tôi Dự Báo Chính Xác Doanh Số 12 Tháng Tới Trong 5 Phút

Xử Lý Lỗi Số NUM Với GEOMEAN

GEOMEAN trả về số NUM khi dữ liệu chứa số âm hoặc số 0. Điều này xảy ra khi tính tỷ lệ tăng trưởng có quý hoặc năm giảm xuống 0 hoặc âm.

Giải pháp 1: Chuyển đổi sang tỷ lệ tăng trưởng dương

Thay vì dùng giá trị thô -10 phần trăm, dùng 0.90 (giảm xuống còn 90 phần trăm giá trị ban đầu).

Thay vì: GEOMEAN(1.2, -0.1, 1.15) → LỖI
Dùng: GEOMEAN(1.2, 0.9, 1.15) → 1.07

Giải pháp 2: Lọc dữ liệu trước khi tính

Kết hợp IF và COUNTIF để kiểm tra điều kiện trước khi áp dụng GEOMEAN.

=IF(COUNTIF(C2:C10,"<=0")>0, "Dữ liệu không hợp lệ", GEOMEAN(C2:C10))

Tôi thêm validation này vào tất cả các template báo cáo sau khi gặp lỗi số NUM trong buổi họp với ban giám đốc. Công thức tự động kiểm tra và thông báo thay vì hiển thị lỗi.

So Sánh Trực Tiếp Với Ví Dụ Thực Tế

Lấy dữ liệu tỷ suất lợi nhuận của quỹ đầu tư qua 5 năm: 12 phần trăm, -5 phần trăm, 18 phần trăm, -8 phần trăm, 22 phần trăm.

Tính toán với AVERAGE:

=AVERAGE(0.12, -0.05, 0.18, -0.08, 0.22)
Kết quả: 7.8%

Tính toán với GEOMEAN:

=GEOMEAN(1.12, 0.95, 1.18, 0.92, 1.22) - 1
Kết quả: 6.9%

Chênh lệch gần 1 phần trăm. Với danh mục 500 triệu trong 5 năm, sai số này tương đương 25 triệu đồng trong dự báo.

Kiểm chứng:

Giả sử đầu tư 100 triệu ban đầu và áp dụng từng tỷ lệ thực tế:

Sau năm 1: 100 × 1.12 = 112 triệu
Sau năm 2: 112 × 0.95 = 106.4 triệu
Sau năm 3: 106.4 × 1.18 = 125.6 triệu
Sau năm 4: 125.6 × 0.92 = 115.5 triệu
Sau năm 5: 115.5 × 1.22 = 140.9 triệu

Tổng tăng trưởng thực tế: 40.9 phần trăm trong 5 năm.

Tỷ lệ tăng trưởng hàng năm thực tế: (140.9/100)^(1/5) – 1 = 7.1 phần trăm

GEOMEAN cho 6.9 phần trăm gần với 7.1 phần trăm thực tế. AVERAGE cho 7.8 phần trăm lệch xa 0.7 điểm phần trăm.

Áp Dụng Vào Bảng Tính Thực Tế

Trong báo cáo phân tích hiệu suất, tôi dùng cả hai hàm tùy loại dữ liệu. Một sheet có thể cần cả AVERAGE và GEOMEAN ở các cột khác nhau.

XEM THÊM: Hàm PROB Giải Quyết Bài Toán Xác Suất Nhanh Hơn 80% So Với Tính Thủ Công

Cấu trúc sheet phân tích:

Cột A: Tháng
Cột B: Doanh thu (số tuyệt đối) → Dùng AVERAGE
Cột C: Tỷ lệ tăng trưởng (phần trăm) → Dùng GEOMEAN
Cột D: Chi phí (số tuyệt đối) → Dùng AVERAGE
Cột E: Tỷ lệ lợi nhuận (phần trăm) → Dùng GEOMEAN

Công thức trong hàng tổng kết:

Doanh thu TB: =AVERAGE(B2:B13)
Tăng trưởng TB: =GEOMEAN(C2:C13)-1
Chi phí TB: =AVERAGE(D2:D13)
Lợi nhuận TB: =GEOMEAN(E2:E13)-1

Template này giúp tôi tránh nhầm lẫn giữa hai loại tính trung bình. Mỗi cột có ghi chú rõ ràng về hàm nào được sử dụng.

Khi Nào Kết Quả Giống Nhau

Có một trường hợp đặc biệt khi AVERAGE và GEOMEAN cho kết quả giống nhau: khi tất cả các số bằng nhau.

Dãy: 5, 5, 5, 5, 5
AVERAGE: 5
GEOMEAN: 5

Với dữ liệu biến động nhỏ, sự khác biệt cũng không đáng kể. Dãy 98, 100, 102 cho AVERAGE là 100 và GEOMEAN là 99.99.

Nhưng khi dữ liệu có độ dao động lớn hoặc chứa giá trị cực trị, sự khác biệt trở nên rõ ràng. Dãy 1, 10, 100 cho AVERAGE là 37 và GEOMEAN là 10. Chênh lệch gấp 3.7 lần.

Nguyên tắc: Nếu các số dao động trong phạm vi 20 phần trăm, cả hai hàm cho kết quả tương tự. Nếu dao động lớn hơn 50 phần trăm, chọn đúng hàm rất quan trọng.

Chọn Hàm Đúng Cho Từng Trường Hợp

Quyết định nhanh dựa trên loại dữ liệu. Nếu dữ liệu là giá trị tuyệt đối độc lập như điểm số, nhiệt độ, khoảng cách, dùng AVERAGE. Nếu dữ liệu là tỷ lệ phần trăm, tốc độ tăng trưởng, lợi nhuận đầu tư hoặc bất kỳ giá trị nào ảnh hưởng lẫn nhau theo thời gian, dùng GEOMEAN.

Checklist lựa chọn:

Dùng AVERAGE khi:

Các giá trị độc lập với nhau
Cộng các giá trị lại có ý nghĩa
Không có tác động kép hay tích lũy
Ví dụ: điểm thi, nhiệt độ hàng ngày, thời gian phản hồi

Dùng GEOMEAN khi:

Giá trị sau phụ thuộc giá trị trước
Dữ liệu là tỷ lệ phần trăm thay đổi
Có tác động lãi kép hoặc tích lũy
Ví dụ: tỷ suất sinh lợi, tốc độ tăng trưởng, lạm phát

Cả hai hàm đều có trong mọi phiên bản Excel từ 2007 trở đi. GEOMEAN cũng hoạt động trong Google Sheets và LibreOffice Calc với cú pháp giống hệt. Nếu làm việc với dữ liệu tài chính hoặc phân tích tăng trưởng, bắt đầu thay thế AVERAGE bằng GEOMEAN ở những chỗ tính phần trăm để có số liệu chính xác hơn.