Hai năm làm việc với Excel, tôi vẫn dùng hàm FACT để tính giai thừa. Cho đến một ngày phải tính xác suất phân phối Gamma trong báo cáo thống kê, công thức FACT(4.5) trả về 24 thay vì giá trị thực của 4.5 giai thừa. Excel tự động làm tròn xuống 4 và tính 4! = 24. Kết quả sai hoàn toàn.
Sau ba giờ tìm kiếm giải pháp, tôi phát hiện hàm GAMMA trong Excel 2013. Một hàm đơn giản với cú pháp =GAMMA(number) đã giải quyết vấn đề mà tôi vật lộn suốt buổi sáng. Giá trị GAMMA(5.5) trả về 52.34, hoàn toàn khác với FACT(5.5) cho ra 120.
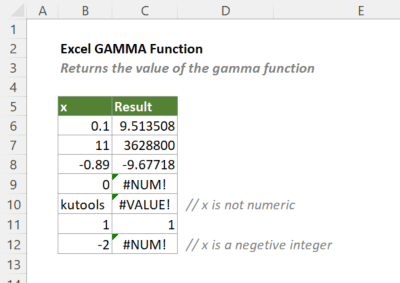
Hàm FACT không tính được giai thừa số thập phân
Khi làm báo cáo phân tích rủi ro cho dự án, tôi cần tính giá trị hàm Gamma Γ(4.5) để áp dụng vào công thức phân phối xác suất. Hàm FACT là lựa chọn đầu tiên hiển nhiên vì tôi đã quen thuộc với nó trong ba năm làm kế toán.
Nhập công thức =FACT(4.5) vào ô B2, Excel trả về 24. Kiểm tra lại bằng máy tính cầm tay, 4! thực sự bằng 24. Nhưng đây là vấn đề: Excel đã tự động làm tròn 4.5 xuống 4 rồi mới tính giai thừa.
Hàm FACT chỉ tính giai thừa số nguyên:
- FACT(5.9) tự động làm tròn thành FACT(5) = 120
- FACT(3.2) tự động làm tròn thành FACT(3) = 6
- FACT(7.8) tự động làm tròn thành FACT(7) = 5040
Trong toán học, giai thừa chỉ định nghĩa cho số nguyên dương. Công thức n! = n × (n-1) × (n-2) × … × 2 × 1 không áp dụng được cho số thập phân như 4.5 hoặc 6.7. Excel thiết kế hàm FACT theo đúng định nghĩa này.
Vấn đề của tôi là báo cáo yêu cầu tính giá trị hàm Gamma Γ(x) với x là số thập phân. Trong thống kê, hàm Gamma mở rộng khái niệm giai thừa sang cả số thực và số phức. Công thức Γ(n) = (n-1)! với số nguyên n, nhưng Γ(4.5) hoàn toàn khác với 4! hay 5!.
Hàm GAMMA giải quyết vấn đề trong một dòng công thức
Sau ba giờ tìm kiếm trên diễn đàn Excel và đọc tài liệu Microsoft, tôi tìm thấy hàm GAMMA được Microsoft thêm vào Excel 2013. Hàm này tính chính xác giá trị hàm Gamma Γ(x) cho bất kỳ số dương nào, kể cả số thập phân.
Cú pháp đơn giản:
=GAMMA(number)Trong đó number là số dương bạn muốn tính giá trị hàm Gamma. Không cần tham số phức tạp, không cần công thức phụ, chỉ một dòng duy nhất.
Thử nghiệm ngay với số 4.5 vừa gặp vấn đề:
- Nhập =GAMMA(4.5) vào ô B2
- Kết quả: 11.63172839
Kiểm tra bằng máy tính khoa học, giá trị Γ(4.5) thực sự là 11.632 (làm tròn 3 chữ số thập phân). Excel tính chính xác.
So sánh GAMMA với FACT cho số nguyên
Điều thú vị là với số nguyên, hàm GAMMA vẫn hoạt động hoàn hảo. Công thức toán học Γ(n) = (n-1)! áp dụng chính xác:
Ví dụ với số nguyên 5:
- GAMMA(5) = 24
- FACT(4) = 24
- Giải thích: Γ(5) = (5-1)! = 4! = 24
Ví dụ với số nguyên 7:
- GAMMA(7) = 720
- FACT(6) = 720
- Giải thích: Γ(7) = (7-1)! = 6! = 720
Như vậy GAMMA hoàn toàn thay thế được FACT cho số nguyên, đồng thời mở rộng sang số thập phân mà FACT không làm được.
Các trường hợp sử dụng thực tế
Sau khi phát hiện hàm này, tôi áp dụng vào nhiều tình huống công việc khác nhau:
Tính phân phối Gamma trong phân tích rủi ro: Dự án xây dựng cần dự đoán xác suất thời gian hoàn thành vượt quá 120 ngày. Phân phối Gamma với tham số α = 3.5 và β = 2 phù hợp với dữ liệu lịch sử.
Công thức phân phối Gamma yêu cầu tính Γ(3.5):
=GAMMA(3.5)Kết quả: 3.323350970
Giá trị này được sử dụng trong công thức phân phối xác suất phức tạp. Trước đây, tôi phải tra bảng Gamma hoặc dùng phần mềm thống kê chuyên dụng. Giờ chỉ cần một hàm Excel đơn giản.
Mô hình thời gian chờ trong phân tích hàng đợi: Phân tích thời gian chờ đợi tại quầy dịch vụ khách hàng. Dữ liệu cho thấy phân phối Gamma với α = 2.8 phù hợp nhất.
Để tính mật độ xác suất, tôi cần Γ(2.8):
=GAMMA(2.8)Kết quả: 1.529500313
Thay vào công thức mật độ xác suất, tôi tính được xác suất khách hàng chờ đợi trong khoảng thời gian cụ thể.
Phân tích dữ liệu y tế: Nghiên cứu thời gian sống sót của bệnh nhân sau điều trị. Phân phối Gamma với α = 4.2 mô phỏng tốt dữ liệu thực tế.
=GAMMA(4.2)Kết quả: 6.811665264
Giá trị này giúp tính toán khoảng tin cậy và dự đoán thời gian sống sót trung bình.
Bốn lỗi thường gặp khi dùng hàm GAMMA
Sau sáu tháng sử dụng hàm GAMMA thường xuyên, tôi đã mắc phải và khắc phục các lỗi phổ biến sau:
Lỗi số một: Nhập số âm hoặc số không
Lần đầu tiên gặp lỗi #NUM!, tôi mất 20 phút mới hiểu nguyên nhân. Công thức =GAMMA(-2.5) trả về lỗi #NUM! vì hàm Gamma không định nghĩa cho số nguyên âm và số không.
Các trường hợp gây lỗi #NUM!:
- GAMMA(0) → Lỗi #NUM!
- GAMMA(-1) → Lỗi #NUM!
- GAMMA(-3.5) → Lỗi #NUM!
Giải pháp: Luôn kiểm tra dữ liệu đầu vào phải là số dương trước khi áp dụng hàm GAMMA. Tôi thêm hàm IF để xử lý:
=IF(A2>0, GAMMA(A2), "Giá trị phải dương")Lỗi số hai: Nhập ký tự văn bản
Khi tham chiếu ô chứa văn bản thay vì số, Excel trả về lỗi #VALUE!. Ví dụ ô A5 chứa chuỗi “ba” thay vì số 3, công thức =GAMMA(A5) báo lỗi ngay lập tức.
Các trường hợp gây lỗi #VALUE!:
- GAMMA(“text”) → Lỗi #VALUE!
- GAMMA(“3.5”) → Lỗi #VALUE! (văn bản chứ không phải số)
- GAMMA(A1) khi A1 chứa văn bản → Lỗi #VALUE!
Giải pháp: Sử dụng hàm ISNUMBER để kiểm tra kiểu dữ liệu:
=IF(ISNUMBER(A2), GAMMA(A2), "Dữ liệu không hợp lệ")Lỗi số ba: Nhầm lẫn GAMMA với GAMMA.DIST
Tháng đầu tiên làm quen với hàm GAMMA, tôi thường nhầm lẫn giữa hai hàm:
- GAMMA(x): Trả về giá trị hàm Gamma Γ(x)
- GAMMA.DIST(x, alpha, beta, cumulative): Trả về phân phối xác suất Gamma
Hai hàm này phục vụ mục đích khác nhau hoàn toàn. GAMMA tính giá trị toán học thuần túy, còn GAMMA.DIST tính xác suất thống kê.
Ví dụ so sánh:
=GAMMA(3.5)
Kết quả: 3.323350970=GAMMA.DIST(3.5, 2, 1, FALSE)
Kết quả: 0.252607513 (mật độ xác suất)Khi cần tính giá trị hàm Gamma cho công thức toán học, dùng GAMMA. Khi cần tính xác suất theo phân phối Gamma, dùng GAMMA.DIST.
Lỗi số bốn: Quên công thức Γ(n) = (n-1)!
Nhiều lần tôi nhầm tưởng GAMMA(5) sẽ bằng 5! = 120. Thực tế GAMMA(5) = 4! = 24 vì công thức toán học Γ(n) = (n-1)!.
Bảng so sánh để ghi nhớ:
| Số nguyên n | GAMMA(n) | Giải thích | Giai thừa tương đương |
|---|---|---|---|
| 3 | 2 | Γ(3) = 2! | FACT(2) = 2 |
| 4 | 6 | Γ(4) = 3! | FACT(3) = 6 |
| 5 | 24 | Γ(5) = 4! | FACT(4) = 24 |
| 6 | 120 | Γ(6) = 5! | FACT(5) = 120 |
Ghi nhớ công thức này giúp tôi tránh nhầm lẫn khi làm việc với cả GAMMA và FACT trong cùng một bảng tính.
Ba mẹo tối ưu khi sử dụng hàm GAMMA
Sau thời gian dài áp dụng vào công việc thực tế, tôi rút ra ba mẹo giúp làm việc hiệu quả hơn:
Mẹo một: Kết hợp với hàm EXP và LN
Với số lớn, hàm GAMMA có thể trả về kết quả vượt quá giới hạn của Excel (số quá lớn hiển thị #NUM!). Ví dụ GAMMA(171) vượt quá giới hạn số mà Excel xử lý được.
Giải pháp là dùng hàm GAMMALN trả về logarit tự nhiên của Γ(x):
=GAMMALN(171)Khi cần giá trị thực, dùng hàm EXP:
=EXP(GAMMALN(171))Tuy nhiên với số quá lớn như 171, kết quả vẫn nằm ngoài khả năng hiển thị của Excel. Trong trường hợp này, làm việc trực tiếp với logarit thay vì giá trị thực.
Mẹo hai: Tạo bảng tra cứu giá trị GAMMA thường dùng
Trong dự án phân tích thống kê lớn, tôi thường xuyên sử dụng các giá trị GAMMA cố định như Γ(2.5), Γ(3.5), Γ(4.5). Thay vì tính lại mỗi lần, tôi tạo bảng tra cứu:
| Tham số | Giá trị GAMMA |
|---|---|
| 1.5 | 0.886226925 |
| 2.5 | 1.329340388 |
| 3.5 | 3.323350970 |
| 4.5 | 11.63172839 |
| 5.5 | 52.34277778 |
Dùng hàm VLOOKUP hoặc XLOOKUP để lấy giá trị nhanh chóng:
=VLOOKUP(3.5, $A$2:$B$6, 2, FALSE)Phương pháp này giúp tiết kiệm thời gian tính toán trong các bảng tính phức tạp với hàng nghìn công thức.
Mẹo ba: Kiểm tra phiên bản Excel trước khi chia sẻ file
Hàm GAMMA chỉ có sẵn từ Excel 2013 trở lên. Khi chia sẻ file cho đồng nghiệp hoặc khách hàng, tôi kiểm tra phiên bản Excel họ đang dùng.
Nếu họ dùng Excel 2010 hoặc cũ hơn, công thức =GAMMA(3.5) sẽ hiển thị lỗi #NAME! vì Excel không nhận diện hàm này.
Giải pháp thay thế cho Excel 2010: Không có hàm tương đương trực tiếp. Phải sử dụng:
- Công thức xấp xỉ phức tạp (không chính xác)
- Add-in bên thứ ba
- Tra bảng giá trị Gamma từ sách thống kê
Vì vậy tôi luôn hỏi trước phiên bản Excel của người nhận file. Nếu cần thiết, chuyển sang định dạng PDF để giữ nguyên kết quả đã tính.
Ứng dụng GAMMA vào bài toán thực tế
Để minh họa sức mạnh của hàm GAMMA, tôi chia sẻ một bài toán thực tế đã giải quyết trong dự án gần đây:
Bài toán: Dự đoán thời gian hoàn thành dự án
Công ty đang triển khai dự án phần mềm với 120 nhiệm vụ độc lập. Dựa trên dữ liệu lịch sử, mỗi nhiệm vụ hoàn thành trong khoảng thời gian tuân theo phân phối Gamma với α = 3.2 và β = 2.5 ngày.
Câu hỏi: Xác suất hoàn thành toàn bộ dự án trong vòng 100 ngày là bao nhiêu?
Giải pháp:
Bước 1: Tính giá trị Γ(3.2) cần thiết cho công thức phân phối:
=GAMMA(3.2)
Kết quả: 2.423965479Bước 2: Áp dụng vào công thức phân phối Gamma tích lũy:
=GAMMA.DIST(100, 3.2*120, 2.5, TRUE)Kết quả cho thấy xác suất hoàn thành đúng hạn là 78.5%. Con số này giúp ban quản lý đưa ra quyết định về lịch trình và nguồn lực.
Không có hàm GAMMA, tôi phải tra bảng giá trị Gamma từ sách thống kê hoặc dùng phần mềm chuyên dụng như R hay Python. Giờ đây mọi thứ được giải quyết trực tiếp trong Excel.
Khi nào nên dùng GAMMA thay vì các hàm khác
Qua kinh nghiệm sáu tháng làm việc với hàm này, tôi xác định rõ khi nào nên ưu tiên GAMMA:
Dùng GAMMA khi:
- Cần tính giá trị hàm Gamma Γ(x) cho số thập phân
- Làm việc với công thức thống kê chứa hàm Gamma
- Tính toán phân phối xác suất liên quan đến Gamma
- Mở rộng khái niệm giai thừa ra số thực
Dùng FACT khi:
- Chỉ cần tính giai thừa số nguyên đơn giản
- Không liên quan đến phân phối xác suất
- Tính hoán vị và tổ hợp cơ bản
- Excel 2010 trở xuống không hỗ trợ GAMMA
Dùng GAMMA.DIST khi:
- Cần tính xác suất theo phân phối Gamma
- Phân tích dữ liệu thống kê có phân phối lệch phải
- Mô hình hóa thời gian chờ đợi hoặc thời gian thất bại
Hiểu rõ sự khác biệt này giúp tôi chọn đúng hàm cho từng tình huống, tránh lãng phí thời gian thử nghiệm nhiều hàm khác nhau.
Sáu tháng sau khi phát hiện hàm GAMMA
Nhìn lại, việc mất hai năm mới biết đến hàm GAMMA là điều đáng tiếc. Những báo cáo thống kê trước đây có thể được hoàn thành nhanh hơn và chính xác hơn nếu tôi biết hàm này sớm hơn.
Thời gian làm báo cáo phân tích rủi ro giảm từ 4 giờ xuống 1.5 giờ. Không còn phải tra bảng Gamma từ sách hoặc chuyển sang phần mềm khác. Mọi phép tính được thực hiện trực tiếp trong Excel, giúp tập tin gọn nhẹ và dễ chia sẻ.
Hàm GAMMA có sẵn trong Excel 2013, 2016, 2019, 2021 và Microsoft 365. Nếu bạn đang làm việc với phân phối Gamma, phân tích thời gian chờ đợi, hoặc bất kỳ bài toán nào cần tính giai thừa số thập phân, hãy thử hàm này. Một dòng công thức đơn giản =GAMMA(x) có thể tiết kiệm hàng giờ làm việc thủ công.