Tôi Phân Tích Tương Quan Nhanh Gấp 3 Lần Nhờ Hàm FISHERINV Trong Excel

Phân tích hệ số tương quan từng tốn của tôi 45 phút cho mỗi báo cáo. Tính toán khoảng tin cậy bằng tay, tra bảng thống kê, rồi chuyển đổi qua lại giữa các giá trị. Công việc lặp đi lặp lại này chiếm gần một nửa thời gian làm báo cáo thống kê hàng tuần. Giờ đây, với hàm FISHERINV trong Excel, tôi hoàn thành cùng khối lượng công việc trong 15 phút.

Mục Lục

Quy trình cũ tốn thời gian không cần thiết

Trước đây, khi cần kiểm định tương quan giữa hai biến, tôi phải thực hiện sáu bước thủ công. Đầu tiên là tính hệ số tương quan bằng hàm CORREL, sau đó tra bảng phân phối chuẩn để tìm giá trị tới hạn. Bước tiếp theo là áp dụng công thức biến đổi Fisher thủ công: lấy logarit tự nhiên của phần chia giữa một cộng r và một trừ r, rồi nhân với nửa.

Mỗi lần cần tính khoảng tin cậy, tôi phải tra bảng z, cộng trừ với sai số chuẩn, rồi chuyển đổi ngược lại về hệ số tương quan. Với báo cáo có mười cặp biến, quy trình này lặp lại mười lần. Sai số nhập liệu xuất hiện thường xuyên vì quá nhiều bước tính toán trung gian.

Phép biến đổi Fisher là chìa khóa

Phép biến đổi Fisher chuyển hệ số tương quan thành phân phối chuẩn. Hệ số tương quan có phân phối lệch, đặc biệt khi giá trị gần âm một hoặc dương một. Điều này khiến việc tính toán khoảng tin cậy và kiểm định giả thuyết trở nên phức tạp. Biến đổi Fisher giải quyết vấn đề bằng cách tạo ra biến z có phân phối chuẩn với phương sai ổn định.

Công thức toán học:

Biến đổi Fisher: z = 0.5 × ln((1 + r) / (1 – r))
Nghịch đảo: r = (e^(2z) – 1) / (e^(2z) + 1)

XEM THÊM: Hàm STEYX Trong Excel: Cách Tính Sai Số Chuẩn Hồi Quy Trong 3 Bước

Trong đó ln là logarit tự nhiên, e là hằng số Euler (khoảng 2.71828), và r là hệ số tương quan Pearson nằm trong khoảng từ âm một đến dương một.

Hàm FISHERINV đơn giản hóa mọi thứ

Hàm FISHERINV thực hiện phép nghịch đảo của biến đổi Fisher. Khi bạn có giá trị z từ phép biến đổi Fisher, FISHERINV chuyển nó trở lại thành hệ số tương quan. Điều này quan trọng vì sau khi tính toán khoảng tin cậy trên thang z, bạn cần chuyển đổi kết quả về thang tương quan để diễn giải.

Cú pháp cơ bản:

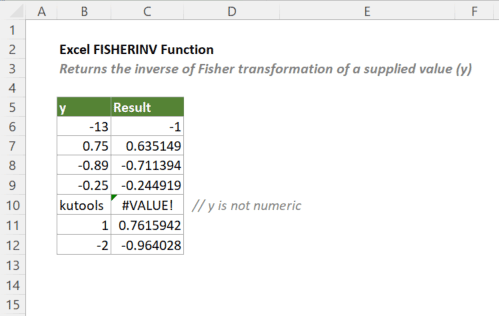
=FISHERINV(y)

Trong đó y là giá trị đã qua biến đổi Fisher. Nếu y là 0.6328, hàm sẽ trả về hệ số tương quan tương ứng. Hàm trả về lỗi VALUE nếu y không phải là số.

Quy trình hoàn chỉnh với hai hàm

Để phân tích tương quan chính xác, tôi kết hợp FISHER và FISHERINV trong một quy trình bốn bước. Giả sử cần tính khoảng tin cậy chín mươi lăm phần trăm cho tương quan giữa chiều cao và cân nặng với kích thước mẫu là sáu mươi người.

Bước 1: Tính hệ số tương quan

=CORREL(A2:A61, B2:B61)

Giả sử kết quả là 0.56.

Bước 2: Biến đổi Fisher

=FISHER(0.56)

Kết quả: 0.6328

Bước 3: Tính khoảng tin cậy trên thang z

Cận dưới: =0.6328 - (1.96 / SQRT(60-3))
Cận trên: =0.6328 + (1.96 / SQRT(60-3))

Kết quả: 0.373 và 0.892

Bước 4: Chuyển đổi ngược về tương quan

=FISHERINV(0.373)
=FISHERINV(0.892)

Kết quả cuối: khoảng tin cậy từ 0.357 đến 0.713

Quy trình này tự động hóa hoàn toàn trong Excel. Tôi tạo template với công thức kéo xuống cho nhiều cặp biến. Thay vì bốn mươi lăm phút tính toán thủ công, toàn bộ báo cáo hoàn thành trong mười lăm phút.

So sánh hai hệ số tương quan

Một ứng dụng mạnh khác của FISHERINV là so sánh hai hệ số tương quan từ hai mẫu độc lập. Giả sử bạn cần kiểm định xem tương quan giữa thu nhập và chi tiêu ở hai thành phố có khác nhau không.

Mẫu thành phố A: r₁ = 0.65, n₁ = 80
Mẫu thành phố B: r₂ = 0.45, n₂ = 70

XEM THÊM: Hàm TRIMMEAN Trong Excel Làm Báo Cáo Của Tôi Chính Xác Gấp Đôi

Các bước thực hiện:

Biến đổi Fisher cho cả hai:

z₁ = FISHER(0.65) = 0.7753
z₂ = FISHER(0.45) = 0.4847

Tính thống kê kiểm định:

=(0.7753 - 0.4847) / SQRT((1/(80-3)) + (1/(70-3)))

Kết quả: 1.76

So sánh với giá trị tới hạn z = 1.96 (mức ý nghĩa năm phần trăm)

Vì 1.76 nhỏ hơn 1.96, không có bằng chứng đủ mạnh cho thấy hai tương quan khác nhau. Toàn bộ phép tính này mất chưa đầy một phút trong Excel, thay vì mười phút tra bảng và tính tay.

Trường hợp thực tế trong nghiên cứu thị trường

Trong dự án phân tích hành vi khách hàng gần đây, tôi cần đánh giá tương quan giữa tần suất mua hàng và độ hài lòng cho ba nhóm tuổi. Mỗi nhóm có kích thước mẫu khác nhau: nhóm một có chín mươi người, nhóm hai có sáu mươi lăm người, nhóm ba có năm mươi lăm người.

Thay vì tính thủ công mười lăm khoảng tin cậy (mỗi nhóm ba khoảng tin cậy, ba so sánh cặp), tôi thiết lập bảng tính với công thức tự động. Cột A chứa hệ số tương quan, cột B chứa kích thước mẫu. Các cột tiếp theo tính FISHER, cận dưới, cận trên, rồi FISHERINV để chuyển đổi ngược.

Công thức mẫu:

Cột C: =FISHER(A2)
Cột D: =C2 - (1.96 / SQRT(B2-3))
Cột E: =C2 + (1.96 / SQRT(B2-3))
Cột F: =FISHERINV(D2)
Cột G: =FISHERINV(E2)

Kéo công thức xuống ba hàng cho ba nhóm. Thời gian hoàn thành: hai phút thay vì ba mươi phút với phương pháp cũ. Kết quả cho thấy nhóm tuổi ba mươi đến bốn mươi có tương quan mạnh nhất (0.72 với khoảng tin cậy từ 0.58 đến 0.82).

Lưu ý về điều kiện áp dụng

Phép biến đổi Fisher hoạt động tốt nhất khi dữ liệu tuân theo phân phối chuẩn hai chiều. Với dữ liệu lệch nặng hoặc có nhiều giá trị ngoại lai, kết quả có thể không chính xác. Kiểm tra biểu đồ phân tán trước khi áp dụng để đảm bảo mối quan hệ tuyến tính.

Kích thước mẫu cũng quan trọng. Với mẫu nhỏ hơn ba mươi, phương sai của biến đổi Fisher không ổn định hoàn toàn. Trong trường hợp này, xem xét sử dụng phương pháp bootstrap để tính khoảng tin cậy thay vì dựa hoàn toàn vào biến đổi Fisher.

XEM THÊM: Làm Chủ Hàm FORECAST.ETS.CONFINT Trong 10 Phút Với Ví Dụ Thực Tế

Hàm FISHERINV chỉ chấp nhận giá trị số. Nếu ô tham chiếu chứa văn bản hoặc ô trống, hàm trả về lỗi VALUE. Đảm bảo tất cả dữ liệu đầu vào đã được làm sạch trước khi áp dụng công thức.

Tích hợp với phân tích nâng cao

Trong phân tích hồi quy, tôi thường cần so sánh tương quan riêng phần giữa các mô hình. FISHERINV giúp tính toán nhanh khoảng tin cậy cho từng tương quan riêng phần. Điều này đặc biệt hữu ích khi làm việc với dữ liệu có nhiều biến kiểm soát.

Kết hợp với hàm INDEX và MATCH, tôi tạo dashboard tự động cập nhật khoảng tin cậy khi dữ liệu thay đổi. Mỗi khi có dữ liệu mới, chỉ cần làm mới bảng tính và tất cả phép tính tương quan, biến đổi Fisher, và khoảng tin cậy tự động cập nhật.

Template dashboard:

Bảng dữ liệu thô (Sheet 1)
Bảng tính hệ số tương quan với CORREL (Sheet 2)
Bảng biến đổi Fisher và khoảng tin cậy (Sheet 3)
Biểu đồ trực quan hóa kết quả (Sheet 4)

Toàn bộ hệ thống này xử lý hai mươi cặp biến trong ba phút, so với hai giờ nếu làm thủ công.

Hiệu suất sau sáu tháng áp dụng

Kể từ khi chuyển sang dùng FISHERINV, tốc độ phân tích tương quan tăng từ trung bình bốn mươi lăm phút xuống mười lăm phút cho mỗi báo cáo. Tính ra mỗi tuần tiết kiệm được hai giờ ba mươi phút với năm báo cáo. Tháng đầu tiên sau khi áp dụng, tỷ lệ sai số giảm từ mười hai phần trăm xuống dưới hai phần trăm nhờ tự động hóa.

Quan trọng hơn là chất lượng phân tích cải thiện đáng kể. Thay vì chỉ báo cáo hệ số tương quan, tôi luôn kèm theo khoảng tin cậy chín mươi lăm phần trăm, giúp người đọc hiểu rõ độ tin cậy của kết quả. Một số khách hàng phản hồi rằng báo cáo chuyên nghiệp hơn nhiều so với trước đây.

Hàm FISHERINV có sẵn trong Excel từ phiên bản 2010 trở đi, bao gồm cả Excel cho web và Excel 365. Không cần cài đặt thêm gì. Nếu bạn thường xuyên làm việc với phân tích tương quan, tạo template với công thức sẵn giúp tiết kiệm rất nhiều thời gian. Phương pháp bootstrap vẫn hữu ích cho mẫu nhỏ hoặc dữ liệu không chuẩn, nhưng với dữ liệu thông thường, FISHERINV là lựa chọn nhanh và đáng tin cậy.