Hàm STEYX Trong Excel: Cách Tính Sai Số Chuẩn Hồi Quy Trong 3 Bước

Tính sai số chuẩn của mô hình hồi quy bằng tay mất ít nhất 10 phút với máy tính cầm tay. Phải tính độ lệch chuẩn, trung bình mẫu, rồi áp dụng công thức phức tạp với căn bậc hai và tổng bình phương. Hàm STEYX trong Excel làm việc này trong 3 giây với độ chính xác tuyệt đối.

Mục Lục

Hàm STEYX là gì và tại sao cần dùng

STEYX tính toán sai số chuẩn của giá trị y dự đoán trong mô hình hồi quy tuyến tính. Đây là thước đo quan trọng cho thấy các điểm dữ liệu thực tế lệch khỏi đường hồi quy bao nhiêu. Giá trị sai số chuẩn càng nhỏ, mô hình dự đoán càng chính xác.

Trong phân tích thống kê, bạn cần biết mô hình hồi quy có đáng tin cậy không trước khi đưa ra quyết định kinh doanh. Một mô hình dự đoán doanh thu với sai số chuẩn 50 triệu đồng và một mô hình khác với sai số chuẩn 5 triệu đồng cho thấy sự khác biệt rõ ràng về độ tin cậy.

Công thức toán học: Hàm STEYX sử dụng công thức: căn bậc hai của [tổng bình phương sai số chia cho (n-2)], trong đó n là số lượng điểm dữ liệu. Excel tính toán tự động thay vì bạn phải làm thủ công.

Bước 1: Chuẩn bị dữ liệu đúng cách

Trước khi dùng hàm STEYX, dữ liệu phải đáp ứng ba yêu cầu cơ bản. Vi phạm một trong ba điều này sẽ dẫn đến lỗi hoặc kết quả sai.

Yêu cầu bắt buộc:

Ít nhất 3 cặp điểm dữ liệu (x, y). Ít hơn 3 điểm sẽ hiển thị lỗi #DIV/0!
Số lượng giá trị x phải bằng số lượng giá trị y. Nếu khác nhau sẽ xuất hiện lỗi #N/A
Dữ liệu phải là số. Ô trống hoặc văn bản trong phạm vi sẽ bị bỏ qua, nhưng ô chứa số 0 vẫn được tính

Tôi thường sắp xếp dữ liệu thành hai cột liền kề: cột A chứa biến độc lập x, cột B chứa biến phụ thuộc y. Điều này giúp dễ kiểm tra và đảm bảo số lượng điểm khớp nhau.

XEM THÊM: Làm Chủ Hàm MAXIFS Excel 2019 Để Phân Tích Dữ Liệu Nhanh Gấp Đôi

Ví dụ cấu trúc dữ liệu:

  A (Giờ học)  |  B (Điểm thi)
      2        |      55
      4        |      65
      6        |      75
      8        |      85
      10       |      95

Với bộ dữ liệu này, ta có 5 cặp điểm, đủ điều kiện để tính sai số chuẩn. Nếu một ô trong cột A hoặc B trống, Excel sẽ tự động bỏ qua cả cặp điểm đó.

Bước 2: Nhập công thức STEYX

Cú pháp của hàm cực kỳ đơn giản với chỉ hai tham số. Không có tham số tùy chọn hay cài đặt phức tạp.

Cú pháp chuẩn:

=STEYX(known_y's, known_x's)

Cách nhập:

Chọn ô muốn hiển thị kết quả sai số chuẩn
Gõ dấu = để bắt đầu công thức
Gõ STEYX rồi mở ngoặc đơn
Chọn phạm vi chứa giá trị y (biến phụ thuộc)
Gõ dấu phẩy
Chọn phạm vi chứa giá trị x (biến độc lập)
Đóng ngoặc và nhấn Enter

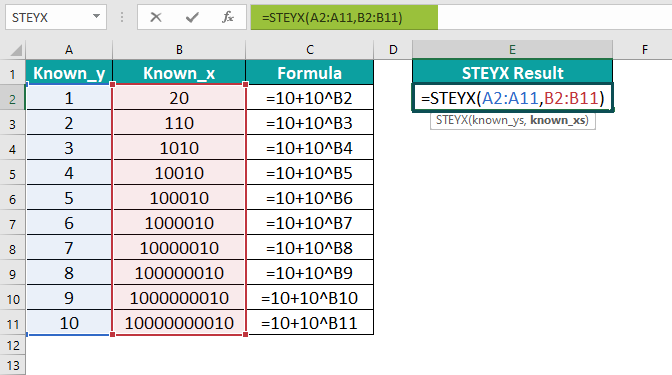
Ví dụ thực tế: Nếu dữ liệu điểm thi nằm trong B2:B6 và giờ học nằm trong A2:A6, công thức sẽ là:

=STEYX(B2:B6, A2:A6)

Lưu ý thứ tự: biến y (điểm thi – kết quả) đứng trước, biến x (giờ học – nguyên nhân) đứng sau. Đảo ngược thứ tự sẽ cho kết quả sai lệch hoàn toàn.

Sau khi nhấn Enter, Excel trả về một giá trị duy nhất. Với ví dụ trên, kết quả khoảng 0 vì các điểm nằm hoàn toàn trên đường thẳng hồi quy. Trong thực tế, dữ liệu sẽ có độ phân tán và sai số chuẩn thường lớn hơn 0.

Bước 3: Đọc và phân tích kết quả

Giá trị mà STEYX trả về là một con số dương thể hiện độ lệch trung bình của các điểm dữ liệu so với đường hồi quy. Việc hiểu ý nghĩa con số này quyết định bạn có thể tin tưởng mô hình hay không.

Nguyên tắc đọc kết quả:

Sai số chuẩn nhỏ (gần 0): Các điểm dữ liệu gần sát đường hồi quy, mô hình dự đoán chính xác cao
Sai số chuẩn lớn: Dữ liệu phân tán xa đường hồi quy, mô hình kém tin cậy
Không có ngưỡng tuyệt đối “tốt” hay “xấu” – phụ thuộc vào ngữ cảnh dữ liệu

Tôi thường so sánh sai số chuẩn với giá trị trung bình của y. Nếu sai số chuẩn bằng 20% giá trị trung bình y trở xuống, mô hình chấp nhận được cho hầu hết mục đích phân tích.

XEM THÊM: Tôi Hiểu Sai Hoàn Toàn Hàm KURT Cho Đến Khi Phân Tích Dữ Liệu Doanh Số

Ví dụ đánh giá thực tế: Giả sử mô hình dự đoán doanh thu cửa hàng dựa trên chi phí quảng cáo:

Doanh thu trung bình: 100 triệu đồng/tháng
STEYX trả về: 5 triệu đồng
Tỷ lệ: 5/100 = 5%

Với sai số chuẩn chỉ 5% doanh thu trung bình, mô hình này rất đáng tin cậy. Nếu STEYX trả về 30 triệu đồng (30%), cần xem xét lại dữ liệu hoặc thêm biến độc lập khác.

Xử lý các lỗi thường gặp

Ba lỗi phổ biến nhất với hàm STEYX đều có nguyên nhân và cách fix cụ thể.

Lỗi #DIV/0! – Không đủ dữ liệu: Xuất hiện khi có ít hơn 3 cặp điểm dữ liệu trong phạm vi. Công thức hồi quy cần tối thiểu 3 điểm để tính toán có ý nghĩa thống kê.

Cách khắc phục: Mở rộng phạm vi dữ liệu hoặc thu thập thêm điểm. Nếu chỉ có 2 điểm, đường hồi quy đi qua chính xác cả hai điểm nên sai số chuẩn không tính được.

Lỗi #N/A – Số lượng không khớp: Xảy ra khi số lượng giá trị trong known_y’s khác với known_x’s. Ví dụ: B2:B10 có 9 giá trị nhưng A2:A11 có 10 giá trị.

Cách khắc phục: Kiểm tra lại phạm vi đã chọn. Dùng Ctrl + Shift + Down Arrow để chọn từ ô đầu đến ô cuối có dữ liệu, đảm bảo cả hai cột có cùng số hàng.

Kết quả lớn bất thường: Nếu STEYX trả về giá trị cực lớn so với phạm vi dữ liệu y, có thể do outliers – những điểm dữ liệu bất thường lệch xa so với nhóm.

Cách khắc phục: Vẽ biểu đồ scatter plot để xác định outliers. Xem xét loại bỏ hoặc điều tra nguyên nhân của những điểm bất thường này trước khi phân tích.

Kết hợp với các hàm hồi quy khác

STEYX hoạt động tốt nhất khi dùng cùng SLOPE, INTERCEPT và RSQ để có bức tranh toàn diện về mô hình hồi quy.

Quy trình phân tích đầy đủ:

=SLOPE(B2:B6, A2:A6)      → Hệ số góc của đường hồi quy
=INTERCEPT(B2:B6, A2:A6)  → Điểm cắt trục y
=RSQ(B2:B6, A2:A6)        → Hệ số R² (độ phù hợp mô hình)
=STEYX(B2:B6, A2:A6)      → Sai số chuẩn (độ chính xác dự đoán)

RSQ cho biết bao nhiêu phần trăm biến thiên của y được giải thích bởi x. RSQ = 0.95 nghĩa là 95% biến thiên được giải thích. STEYX bổ sung thông tin về độ chính xác tuyệt đối của dự đoán.

XEM THÊM: 3 Bước Làm Chủ Hàm NORM.S.INV Trong Phân Tích Thống Kê Excel

Tôi thường tạo một bảng tổng hợp với cả bốn giá trị này. Nếu RSQ cao (trên 0.8) nhưng STEYX lớn, có thể do dữ liệu có phạm vi rộng. Nếu RSQ thấp và STEYX lớn, mô hình cần cải thiện hoặc thay đổi.

Ứng dụng trong phân tích dữ liệu thực tế

Hàm STEYX hữu ích nhất trong ba tình huống phổ biến: đánh giá mô hình dự đoán, so sánh nhiều mô hình và tính khoảng tin cậy.

Đánh giá độ tin cậy dự đoán: Trước khi dùng phương trình hồi quy để dự báo, tính STEYX để biết độ lệch dự kiến. Nếu dự đoán doanh thu tháng sau là 120 triệu với STEYX = 8 triệu, phạm vi thực tế có thể từ 112-128 triệu (±1 sai số chuẩn).

So sánh các mô hình: Khi có nhiều biến độc lập, tính STEYX cho từng mô hình riêng lẻ. Mô hình nào có STEYX nhỏ nhất thường là lựa chọn tốt hơn, giả sử các mô hình có cùng số lượng biến.

Kiểm soát chất lượng: Trong sản xuất, nếu mối quan hệ giữa nhiệt độ lò và độ bền sản phẩm có STEYX tăng đột ngột, báo hiệu quy trình không ổn định cần điều tra ngay.

Hạn chế cần biết

STEYX chỉ áp dụng cho mô hình hồi quy tuyến tính đơn giản. Nếu mối quan hệ giữa x và y không phải đường thẳng, kết quả sẽ không có ý nghĩa.

Hàm này không hoạt động với hồi quy đa biến (nhiều biến x). Với nhiều biến độc lập, cần dùng công cụ Data Analysis Toolpak trong Excel hoặc phần mềm thống kê chuyên dụng như SPSS.

Các ô trống trong phạm vi được bỏ qua tự động, nhưng điều này có thể gây hiểu lầm. Nếu dữ liệu có nhiều ô trống, nên loại bỏ hoặc điền giá trị trước khi phân tích để tránh kết quả không đúng với kỳ vọng.

Tương thích và phiên bản

Hàm STEYX có sẵn trong Excel 2007 trở về sau, bao gồm Excel 2010, 2013, 2016, 2019, 2021 và Microsoft 365. Không cần add-in hay activation đặc biệt.

Hàm hoạt động giống hệt nhau trên Windows và Mac. Cú pháp và kết quả không thay đổi giữa các phiên bản Excel, nên file có công thức STEYX mở trên bất kỳ máy nào cũng tính toán nhất quán.

Với Google Sheets, dùng hàm STEYX với cú pháp hoàn toàn tương tự. Kết quả có thể khác nhau ở chữ số thập phân thứ 10-12 do cách làm tròn, nhưng không ảnh hưởng đáng kể đến phân tích thực tế.