Tôi Đã Hiểu Hàm HYPGEOM.DIST Sau Khi Áp Dụng Vào 3 Tình Huống Thực Tế Này

Hàm HYPGEOM.DIST trong Excel là một trong những hàm xác suất ít người biết đến nhưng cực kỳ hữu ích. Trong hai năm làm việc với dữ liệu thống kê, tôi luôn dùng BINOM.DIST cho mọi bài toán xác suất. Mãi đến khi gặp tình huống kiểm tra chất lượng sản phẩm mà công thức của tôi cho kết quả sai lệch hoàn toàn, tôi mới phát hiện ra HYPGEOM.DIST. Ba tình huống dưới đây giúp tôi hiểu rõ khi nào cần dùng hàm này thay vì các hàm xác suất khác.

Mục Lục

Tình Huống 1: Kiểm Tra Chất Lượng Lô Hàng Điện Thoại

Tính xác suất tìm thấy sản phẩm lỗi trong mẫu kiểm tra

Đây là tình huống thực tế khiến tôi khám phá ra HYPGEOM.DIST. Công ty nhận một lô 500 điện thoại, trong đó có 30 máy bị lỗi màn hình. Phòng kiểm định chất lượng chọn ngẫu nhiên 20 máy để kiểm tra. Câu hỏi đặt ra: xác suất để tìm thấy đúng 2 máy lỗi trong 20 máy được chọn là bao nhiêu?

Tôi ban đầu dùng BINOM.DIST nhưng kết quả không khớp với thực tế. Vấn đề nằm ở chỗ BINOM.DIST giả định rằng sau mỗi lần kiểm tra, xác suất vẫn giữ nguyên. Nhưng trong thực tế, khi đã lấy một máy ra khỏi lô, tổng số máy giảm từ 500 xuống 499, và xác suất thay đổi cho lần kiểm tra tiếp theo. Đây chính là lấy mẫu không hoàn lại.

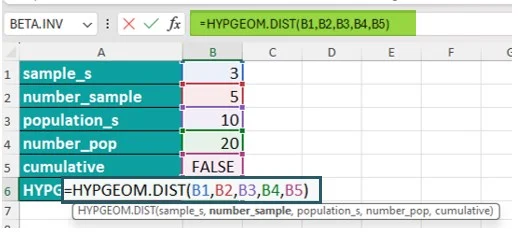
Công thức HYPGEOM.DIST cho tình huống này:

=HYPGEOM.DIST(2, 20, 30, 500, FALSE)

Trong đó:

2: số máy lỗi muốn tìm thấy trong mẫu
20: kích thước mẫu kiểm tra
30: tổng số máy lỗi trong toàn bộ lô hàng
500: tổng số máy trong lô hàng
FALSE: tính xác suất chính xác, không phải tích lũy

Kết quả trả về 0.2638 hay 26.38%. Con số này cho biết khả năng tìm thấy đúng 2 máy lỗi trong 20 máy kiểm tra là khoảng 1 trên 4. Khi tôi đổi sang TRUE để tính xác suất tích lũy, hàm trả về 0.9394 nghĩa là có 93.94% khả năng tìm thấy không quá 2 máy lỗi.

Điểm quan trọng: nếu dùng sai BINOM.DIST cho tình huống này, kết quả sẽ lệch khoảng 3-5% so với thực tế. Với các quyết định nghiệm thu hàng trị giá hàng tỷ đồng, sai số này có thể gây hậu quả lớn.

Tình Huống 2: Rút Thẻ Bài Từ Bộ Bài Tây

Hiểu rõ sự khác biệt giữa TRUE và FALSE

Sau khi áp dụng thành công ở tình huống 1, tôi muốn hiểu sâu hơn về tham số cumulative. Tôi dùng ví dụ quen thuộc: một bộ bài tây 52 lá có 13 lá cơ. Nếu rút ngẫu nhiên 5 lá từ bộ bài, xác suất để có đúng 2 lá cơ là bao nhiêu?

XEM THÊM: Hàm TREND Giúp Tôi Dự Báo Doanh Số 3 Tháng Tiếp Theo Chỉ Trong 30 Giây

Công thức với FALSE để tính xác suất chính xác:

=HYPGEOM.DIST(2, 5, 13, 52, FALSE)

Kết quả: 0.2743 hay 27.43%

Công thức với TRUE để tính xác suất tích lũy:

=HYPGEOM.DIST(2, 5, 13, 52, TRUE)

Kết quả: 0.7547 hay 75.47%

Sự khác biệt rất rõ ràng. FALSE trả về xác suất có đúng 2 lá cơ, trong khi TRUE trả về xác suất có không quá 2 lá cơ, tức là tổng xác suất của các trường hợp có 0, 1, hoặc 2 lá cơ.

Tôi từng mắc lỗi dùng FALSE khi cần TRUE trong một báo cáo phân tích rủi ro. Báo cáo cần biết xác suất để số lỗi không vượt quá mức cho phép, nhưng tôi lại tính xác suất cho số lỗi chính xác bằng mức đó. May mắn phát hiện kịp trước khi trình lãnh đạo.

Quy tắc nhớ đơn giản:

FALSE: xác suất bằng đúng số đó
TRUE: xác suất không vượt quá số đó

Tình Huống 3: Phân Tích Khảo Sát Khách Hàng

Áp dụng vào bài toán thực tế phức tạp hơn

Đây là tình huống phức tạp nhất và giúp tôi thành thạo HYPGEOM.DIST. Công ty có 1000 khách hàng, trong đó 150 người từng khiếu nại về dịch vụ. Bộ phận chăm sóc khách hàng gọi điện khảo sát 50 người được chọn ngẫu nhiên. Họ muốn biết xác suất để trong 50 người này có ít nhất 10 người từng khiếu nại.

Bài toán này cần tư duy ngược. Hàm HYPGEOM.DIST với TRUE chỉ tính được xác suất không quá một số nào đó, không tính được xác suất ít nhất. Giải pháp là dùng công thức bù:

Xác suất ít nhất 10 người = 1 – xác suất không quá 9 người

=1-HYPGEOM.DIST(9, 50, 150, 1000, TRUE)

Kết quả: 0.1834 hay 18.34%

Công thức này trả về khoảng 18% khả năng trong 50 cuộc gọi sẽ có ít nhất 10 người từng khiếu nại. Con số này giúp bộ phận lập kế hoạch nguồn lực xử lý khiếu nại phù hợp.

Tôi cũng tạo thêm bảng phân tích xác suất cho các trường hợp khác nhau:

A1: Số người khiếu nại trong mẫu
B1: Xác suất chính xác (FALSE)
C1: Xác suất tích lũy (TRUE)

A2: 5
B2: =HYPGEOM.DIST(A2, 50, 150, 1000, FALSE)
C2: =HYPGEOM.DIST(A2, 50, 150, 1000, TRUE)

Kéo công thức xuống từ hàng 2 đến hàng 20 để xem phân bố xác suất từ 5 đến 20 người khiếu nại. Biểu đồ này giúp dự đoán kịch bản xấu nhất và chuẩn bị phương án ứng phó.

Các Lỗi Thường Gặp Và Cách Khắc Phục

Qua ba tình huống trên, tôi gặp và xử lý được các lỗi phổ biến khi dùng HYPGEOM.DIST.

Lỗi #NUM! xuất hiện khi:

Số thành công trong mẫu lớn hơn kích thước mẫu
Số thành công trong mẫu lớn hơn tổng số thành công trong quần thể
Kích thước mẫu lớn hơn kích thước quần thể

Ví dụ công thức sai: =HYPGEOM.DIST(25, 20, 30, 500, FALSE) sẽ báo lỗi vì không thể có 25 thành công trong mẫu chỉ gồm 20 phần tử.

XEM THÊM: Cách Dùng Hàm COUNTIFS Để Thống Kê Nhân Viên Nam Trên 25 Ngày Công Trong 1 Nốt Nhạc

Lỗi #VALUE! xuất hiện khi:

Bất kỳ tham số nào không phải là số
Quên nhập tham số cumulative

Cách fix: đảm bảo tất cả các giá trị đều là số nguyên hoặc tham chiếu đến ô chứa số. Excel tự động làm tròn các số thập phân xuống số nguyên gần nhất.

Nhầm lẫn giữa HYPGEOM.DIST và BINOM.DIST:

HYPGEOM.DIST dùng khi:

Lấy mẫu không hoàn lại
Tổng số quần thể hữu hạn và tương đối nhỏ
Mỗi lần lấy mẫu làm thay đổi xác suất lần sau

BINOM.DIST dùng khi:

Lấy mẫu có hoàn lại
Tổng số quần thể vô hạn hoặc rất lớn
Xác suất mỗi lần thử không đổi

Quy tắc nhanh: nếu kích thước mẫu nhỏ hơn 5% kích thước quần thể, hai hàm cho kết quả gần giống nhau. Khi kích thước mẫu lớn hơn 10% kích thước quần thể, sự khác biệt trở nên rõ rệt và HYPGEOM.DIST chính xác hơn.

Mẹo Tối Ưu Khi Sử Dụng

Sau ba năm làm việc với HYPGEOM.DIST, tôi tổng hợp được một số mẹo giúp công việc hiệu quả hơn.

Tạo bảng tra cứu nhanh:

Thay vì tính toán mỗi lần, tôi tạo sẵn bảng tính xác suất cho các kịch bản thường gặp. Bảng này dùng hai chiều với số thành công trong mẫu ở cột đầu và kích thước mẫu ở hàng đầu. Mỗi ô chứa công thức HYPGEOM.DIST tương ứng. Khi cần tra cứu, chỉ việc tìm giao điểm của hàng và cột.

Kết hợp với hàm IF để phân loại:

=IF(HYPGEOM.DIST(10, 50, 150, 1000, FALSE)>0.05, "Cao", "Thấp")

Công thức này tự động phân loại mức độ rủi ro dựa trên xác suất. Nếu xác suất lớn hơn 5% thì cảnh báo rủi ro cao, ngược lại là thấp.

Dùng với bảng tham chiếu:

Thay vì nhập cứng các giá trị, tôi để chúng trong các ô riêng:

A1: Số thành công trong mẫu = 2
A2: Kích thước mẫu = 20
A3: Tổng thành công trong quần thể = 30
A4: Kích thước quần thể = 500
A5: =HYPGEOM.DIST(A1, A2, A3, A4, FALSE)

Cách này cho phép thay đổi các giá trị dễ dàng và xem kết quả cập nhật tức thì. Đặc biệt hữu ích khi chạy phân tích giả lập với nhiều kịch bản khác nhau.

Khi Nào Không Nên Dùng HYPGEOM.DIST

Qua kinh nghiệm, tôi học được rằng HYPGEOM.DIST không phải lúc nào cũng là lựa chọn tốt nhất.

Quần thể quá lớn: Khi kích thước quần thể trên 10,000 phần tử và mẫu nhỏ hơn 100, sự khác biệt giữa HYPGEOM.DIST và BINOM.DIST không đáng kể. BINOM.DIST tính toán nhanh hơn và dễ hiểu hơn trong trường hợp này.

Dữ liệu thay đổi liên tục: HYPGEOM.DIST phù hợp với quần thể cố định. Nếu dữ liệu thay đổi theo thời gian thực, cần dùng các phương pháp thống kê khác như phân tích chuỗi thời gian.

Xác suất phụ thuộc vào điều kiện khác: Hàm này giả định mỗi phần tử trong quần thể có cơ hội được chọn như nhau. Nếu có yếu tố ưu tiên hoặc trọng số khác nhau, HYPGEOM.DIST không còn chính xác.

XEM THÊM: Hàm COUNTA Trong Excel: Đếm Ô Không Trống Chỉ Với 1 Công Thức

So Sánh Với Các Hàm Xác Suất Khác

Hiểu rõ khi nào dùng hàm nào giúp tôi tiết kiệm hàng giờ phân tích sai.

HYPGEOM.DIST vs BINOM.DIST:

HYPGEOM.DIST: lấy mẫu không hoàn lại, xác suất thay đổi
BINOM.DIST: lấy mẫu có hoàn lại, xác suất cố định
Ví dụ thực tế: kiểm tra sản phẩm trong lô hàng dùng HYPGEOM.DIST, tung đồng xu nhiều lần dùng BINOM.DIST

HYPGEOM.DIST vs POISSON.DIST:

HYPGEOM.DIST: quần thể hữu hạn, lấy mẫu không hoàn lại
POISSON.DIST: tính xác suất sự kiện xảy ra trong khoảng thời gian hoặc không gian
Ví dụ thực tế: chọn bi từ hộp dùng HYPGEOM.DIST, số cuộc gọi đến tổng đài mỗi giờ dùng POISSON.DIST

HYPGEOM.DIST vs NORM.DIST:

HYPGEOM.DIST: phân phối rời rạc, số lượng đếm được
NORM.DIST: phân phối liên tục, giá trị đo lường
Ví dụ thực tế: số sản phẩm lỗi dùng HYPGEOM.DIST, chiều cao trung bình dùng NORM.DIST

Ứng Dụng Nâng Cao Trong Công Việc

Ba tình huống ban đầu chỉ là khởi đầu. Sau khi thành thạo, tôi áp dụng HYPGEOM.DIST vào nhiều bài toán phức tạp hơn.

Phân tích rủi ro dự án: Trong một dự án có 30 nhiệm vụ, biết rằng có 8 nhiệm vụ có rủi ro cao. Nếu chọn ngẫu nhiên 10 nhiệm vụ để kiểm tra chi tiết, xác suất phát hiện ít nhất 3 nhiệm vụ rủi ro cao là bao nhiêu? Công thức =1-HYPGEOM.DIST(2, 10, 8, 30, TRUE) cho ra kết quả 44.76%, giúp quyết định có nên tăng số lượng nhiệm vụ kiểm tra hay không.

Tối ưu kế hoạch kiểm định: Công ty cần quyết định nên kiểm tra bao nhiêu sản phẩm để đảm bảo 95% khả năng phát hiện lỗi nếu tỷ lệ lỗi thực tế là 10%. Tôi tạo bảng tính với các kích thước mẫu khác nhau từ 10 đến 100, dùng HYPGEOM.DIST để tính xác suất phát hiện ít nhất 1 lỗi. Kết quả cho thấy mẫu 30 sản phẩm đủ đáp ứng yêu cầu mà không lãng phí nguồn lực.

Dự đoán trong tuyển dụng: Nếu có 200 hồ sơ ứng tuyển trong đó 50 người đạt tiêu chuẩn xuất sắc, và phòng nhân sự chỉ có thể phỏng vấn 20 người, xác suất để có ít nhất 8 người xuất sắc trong số này là bao nhiêu? Công thức =1-HYPGEOM.DIST(7, 20, 50, 200, TRUE) trả về 8.23%, giúp điều chỉnh tiêu chí sơ tuyển hoặc tăng số người phỏng vấn.

Tương Thích Và Phiên Bản

HYPGEOM.DIST có sẵn từ Excel 2010 trở về sau, bao gồm Excel 2013, 2016, 2019, 2021 và Microsoft 365. Hàm này thay thế cho HYPGEOMDIST cũ với độ chính xác được cải thiện. Nếu đang dùng Excel 2007 trở về trước, chỉ có thể dùng HYPGEOMDIST với cú pháp khác một chút và không có tham số cumulative.

Ba tình huống trên giúp tôi chuyển từ việc chỉ biết công thức sang hiểu rõ bản chất của bài toán xác suất. Giờ đây mỗi khi gặp vấn đề liên quan đến lấy mẫu, tôi tự hỏi: quần thể có hữu hạn không? Lấy mẫu có hoàn lại không? Câu trả lời quyết định xem HYPGEOM.DIST có phải công cụ phù hợp hay không. Bắt đầu với một tình huống đơn giản như rút bài hoặc kiểm tra sản phẩm, rồi từ đó mở rộng sang các ứng dụng phức tạp hơn trong công việc thực tế.