Hàm QUARTILE.EXC Trong Excel: Hướng Dẫn Chi Tiết Từ Cú Pháp Đến Ứng Dụng Thực Tế

Phân tích dữ liệu bán hàng theo nhóm khách hàng trở nên đơn giản hơn nhiều khi biết cách dùng đúng hàm tứ phân vị. Hàm QUARTILE.EXC trong Excel tính toán các mốc phần trăm chính xác hơn so với phiên bản cũ, đặc biệt khi làm việc với tập dữ liệu nhỏ. Nhiều người vẫn dùng hàm QUARTILE cũ hoặc nhầm lẫn giữa QUARTILE.EXC và QUARTILE.INC mà không biết sự khác biệt ảnh hưởng đến kết quả như thế nào.

Mục Lục

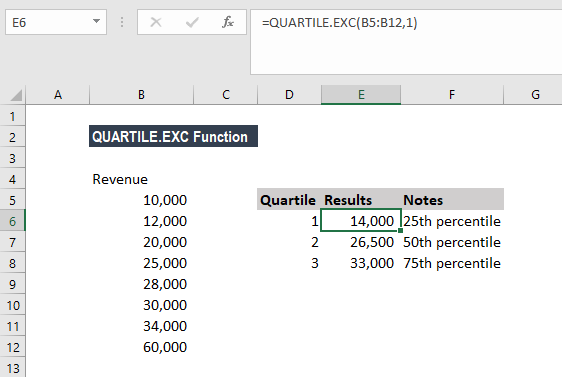
Cú pháp và tham số chính xác

Hàm QUARTILE.EXC có cú pháp đơn giản với hai tham số bắt buộc:

=QUARTILE.EXC(array, quart)

Tham số array: Phạm vi ô hoặc mảng chứa dữ liệu số cần phân tích. Có thể là A1:A50, dữ liệu nhập trực tiếp, hoặc tham chiếu đến vùng đã đặt tên. Hàm bỏ qua các ô trống và văn bản.

Tham số quart: Số nguyên từ 1 đến 3 xác định mốc tứ phân vị cần tính:

1 = Tứ phân vị thứ nhất (phân vị 25%)
2 = Tứ phân vị thứ hai (phân vị 50%, giống trung vị)
3 = Tứ phân vị thứ ba (phân vị 75%)

Điểm quan trọng: QUARTILE.EXC không chấp nhận giá trị 0 hoặc 4 cho tham số quart, khác với QUARTILE.INC. Nếu nhập 0 hoặc 4, hàm trả về lỗi #NUM!.

XEM THÊM: Hàm LOGEST Trong Excel: Hướng Dẫn Đầy Đủ Để Phân Tích Hồi Quy Mũ Với Ví Dụ Thực Tế

Cách sử dụng cơ bản với ví dụ cụ thể

Giả sử bạn có dữ liệu doanh thu tháng của 20 nhân viên bán hàng trong cột B2:B21. Để tìm các mốc phân vị:

Tìm tứ phân vị thứ nhất (25%):

=QUARTILE.EXC(B2:B21, 1)

Kết quả cho biết 25% nhân viên có doanh thu dưới mức này.

Tìm trung vị (50%):

=QUARTILE.EXC(B2:B21, 2)

Giá trị ở giữa tập dữ liệu, chia đôi nhóm nhân viên.

Tìm tứ phân vị thứ ba (75%):

=QUARTILE.EXC(B2:B21, 3)

Chỉ 25% nhân viên vượt qua mốc này.

Để tạo bảng phân tích nhanh, tôi thường setup một bảng nhỏ với công thức kéo xuống. Đặt các giá trị 1, 2, 3 vào cột D3:D5, công thức tại E3 là =QUARTILE.EXC($B$2:$B$21, D3), rồi kéo xuống E4 và E5. Bảng tự động cập nhật khi dữ liệu thay đổi.

Sự khác biệt giữa QUARTILE.EXC và QUARTILE.INC

Cả hai hàm đều tính tứ phân vị nhưng dùng phương pháp khác nhau, dẫn đến kết quả khác với tập dữ liệu nhỏ.

QUARTILE.EXC (exclusive – loại trừ):

Sử dụng công thức: Vị trí = (n + 1) × (phân vị/100)
Loại trừ giá trị nhỏ nhất và lớn nhất khi tính Q1 và Q3
Không tính được phân vị 0% và 100%
Yêu cầu tối thiểu 3 giá trị cho quart = 1 hoặc 3

QUARTILE.INC (inclusive – bao gồm):

Sử dụng công thức: Vị trí = (n – 1) × (phân vị/100) + 1
Bao gồm cả giá trị nhỏ nhất và lớn nhất
Có thể tính phân vị 0% (MIN) và 100% (MAX)
Chấp nhận quart từ 0 đến 4

XEM THÊM: Hàm COUNT Trong Excel Chỉ Đếm Số - Đây Là Lý Do Kết Quả Của Tôi Cứ Ra 0

Với tập dữ liệu: 5, 7, 10, 15, 23, 28, 30

QUARTILE.EXC(dữ liệu, 1) = 7
QUARTILE.INC(dữ liệu, 1) = 7.5

Chênh lệch 0.5 có vẻ nhỏ nhưng ảnh hưởng đến phân nhóm khách hàng hoặc đánh giá hiệu suất. Trong phân tích thống kê chuyên nghiệp, QUARTILE.EXC thường được ưu tiên vì phù hợp với phương pháp Tukey và các công cụ thống kê khác như R và Python.

Bốn lỗi phổ biến và cách khắc phục

Lỗi #NUM! do tham số quart không hợp lệ

Xảy ra khi nhập quart = 0, quart = 4, hoặc quart > 4. Chỉ dùng 1, 2, hoặc 3.

=QUARTILE.EXC(A1:A10, 4)  ❌ Lỗi #NUM!
=QUARTILE.EXC(A1:A10, 3)  ✅ Đúng

Lỗi #NUM! do dữ liệu quá ít

Hàm cần tối thiểu 3 giá trị khi quart = 1 hoặc 3. Với 2 giá trị, chỉ tính được quart = 2 (trung vị).

Dữ liệu A1:A2 chỉ có 2 số
=QUARTILE.EXC(A1:A2, 1)  ❌ Lỗi #NUM!
=QUARTILE.EXC(A1:A2, 2)  ✅ Đúng (trung vị)

Lỗi #VALUE! do tham số không phải số

Xảy ra khi tham chiếu ô chứa văn bản thay vì số trong tham số quart.

Ô D1 chứa văn bản "1"
=QUARTILE.EXC(A1:A10, D1)  ❌ Lỗi #VALUE!
=QUARTILE.EXC(A1:A10, 1)   ✅ Đúng

Array trống hoặc toàn văn bản

Nếu vùng chọn không có giá trị số nào, hàm trả về #NUM!. Kiểm tra lại phạm vi đã chọn đúng cột dữ liệu chưa.

Ứng dụng thực tế trong phân tích dữ liệu

Phân nhóm khách hàng theo doanh thu

Dùng ba mốc tứ phân vị để chia khách hàng thành 4 nhóm: thấp, trung bình thấp, trung bình cao, cao. Tạo cột phân loại bằng hàm IF lồng nhau:

=IF(B2<$E$1, "Thấp", IF(B2<$E$2, "TB Thấp", IF(B2<$E$3, "TB Cao", "Cao")))

Trong đó E1, E2, E3 chứa kết quả QUARTILE.EXC với quart 1, 2, 3.

XEM THÊM: Hàm TRIMMEAN Trong Excel Làm Báo Cáo Của Tôi Chính Xác Gấp Đôi

Phát hiện ngoại lệ với phương pháp IQR

Khoảng tứ phân vị (IQR) = Q3 – Q1 giúp xác định dữ liệu bất thường. Giá trị được coi là ngoại lệ nếu:

Nhỏ hơn Q1 – 1.5 × IQR
Lớn hơn Q3 + 1.5 × IQR

Thiết lập công thức:

Q1: =QUARTILE.EXC(A:A, 1)
Q3: =QUARTILE.EXC(A:A, 3)
IQR: =Q3 - Q1
Ngưỡng dưới: =Q1 - 1.5 * IQR
Ngưỡng trên: =Q3 + 1.5 * IQR

Dùng định dạng có điều kiện để làm nổi các giá trị ngoại lệ. Phương pháp này hiệu quả hơn so với chỉ dùng trung bình và độ lệch chuẩn khi dữ liệu không phân phối chuẩn.

Đánh giá hiệu suất nhân viên

Thay vì so sánh với trung bình, dùng tứ phân vị phản ánh chính xác vị trí trong nhóm. Nhân viên ở Q3 thuộc top 25%, ngay cả khi một vài người có hiệu suất cực cao kéo trung bình lên cao.

Tương thích và lưu ý phiên bản

Hàm QUARTILE.EXC có sẵn từ Excel 2010 trở đi, bao gồm Excel 2013, 2016, 2019, 2021, và Excel 365. Không khả dụng trong Excel 2007 hoặc cũ hơn.

Nếu file cần tương thích ngược với Excel 2007, dùng hàm QUARTILE thay thế. Lưu ý hàm QUARTILE cho kết quả giống QUARTILE.INC, không phải QUARTILE.EXC.

Khi chia sẻ file với người dùng Excel online hoặc Excel mobile, các hàm tứ phân vị hoạt động bình thường. Tuy nhiên, nên test trên nhiều nền tảng trước khi gửi báo cáo quan trọng, đặc biệt với công thức phức tạp kết hợp nhiều hàm.

Đối với tập dữ liệu lớn hơn 10,000 hàng, QUARTILE.EXC tính toán tức thì. Không cần lo về hiệu suất trừ khi dùng hàng trăm công thức cùng lúc trong workbook.