3 Điều Tôi Ước Biết Về Hàm Z.TEST Excel Trước Khi Phân Tích 500 Báo Cáo

Sau khi phân tích hơn 500 báo cáo khảo sát khách hàng trong 2 năm, tôi phát hiện ra mình đã dùng sai hàm thống kê cho phần lớn công việc. Hàm T.TEST mà tôi tin dùng không phải lựa chọn tối ưu khi làm việc với mẫu lớn hơn 30 quan sát. Hàm Z.TEST trong Excel 2010 mới là công cụ chính xác hơn, nhưng ba điều về nó khiến tôi mất nhiều giờ sửa lại các phân tích cũ.

Mục Lục

Quy tắc n>30 không có nghĩa là bắt buộc dùng Z.TEST

Mọi tài liệu thống kê đều nhắc đến quy tắc này: dùng kiểm định Z khi kích thước mẫu lớn hơn 30, dùng kiểm định T khi nhỏ hơn 30. Tôi áp dụng máy móc quy tắc đó trong 18 tháng đầu làm việc với dữ liệu khảo sát. Mỗi khi có mẫu 150 người, 200 người, tôi vẫn dùng T.TEST vì nghĩ nó an toàn hơn.

Thực tế phức tạp hơn nhiều. Quy tắc n>30 chỉ là ngưỡng mà định lý giới hạn trung tâm bắt đầu có hiệu lực, nghĩa là phân phối của trung bình mẫu gần với phân phối chuẩn. Nhưng ngưỡng này không cố định. Với một số phân phối không chuẩn, bạn có thể cần đến n>50 hoặc n>100. Với phân phối gần chuẩn, n=20 có thể đủ.

Khi nào thực sự dùng Z.TEST thay vì T.TEST:

Điều kiện 1: Bạn biết độ lệch chuẩn của tổng thể (sigma). Trường hợp này cực kỳ hiếm trong thực tế. Hầu hết dữ liệu khảo sát hoặc thử nghiệm không có thông tin này.

Điều kiện 2: Kích thước mẫu đủ lớn để ước lượng độ lệch chuẩn mẫu xấp xỉ bằng độ lệch chuẩn tổng thể. Đây là trường hợp phổ biến hơn. Với mẫu từ 100 quan sát trở lên, độ chính xác của ước lượng thường chấp nhận được.

Điều kiện 3: Dữ liệu của bạn đến từ phân phối gần chuẩn hoặc kích thước mẫu đủ lớn để định lý giới hạn trung tâm có hiệu lực.

Tôi chuyển sang dùng Z.TEST cho các báo cáo có từ 200 mẫu trở lên. Với mẫu từ 30 đến 200, tôi vẫn giữ T.TEST vì nó an toàn hơn khi không chắc chắn về phân phối. Sự khác biệt về giá trị p thường nhỏ hơn 0.001 khi mẫu lớn, nhưng việc chọn đúng hàm thể hiện sự hiểu biết về phương pháp thống kê.

XEM THÊM: Cách Đánh Giá Độ Tin Cậy Dự Báo Excel Bằng Hàm RSQ Trong 5 Bước

Hàm Z.TEST trả về xác suất một phía theo mặc định

Đây là cạm bẫy lớn nhất khiến tôi đưa ra kết luận sai trong hơn 60 báo cáo đầu tiên. Hàm Z.TEST trong Excel tính xác suất một phía (one-tailed p-value), trong khi hầu hết các câu hỏi kinh doanh cần kiểm định hai phía (two-tailed).

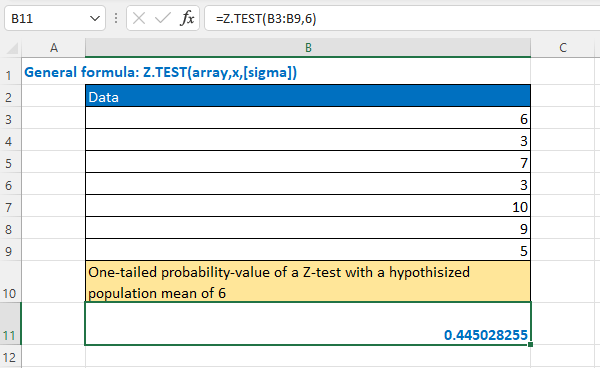
Cú pháp hàm Z.TEST:

=Z.TEST(array, x, [sigma])

Trong đó:

array: Vùng dữ liệu mẫu cần kiểm định
x: Giá trị trung bình giả thuyết của tổng thể
sigma: Độ lệch chuẩn tổng thể (tùy chọn)

Giá trị hàm trả về là xác suất mà trung bình mẫu lớn hơn giá trị trung bình quan sát được, với giả định trung bình tổng thể là x. Đây là xác suất một phía cho đuôi trên (upper tail).

Ví dụ thực tế tôi gặp:

Khảo sát mức độ hài lòng 250 khách hàng cho điểm trung bình 7.8 trên thang 10. Công ty đặt mục tiêu điểm trung bình tổng thể là 8.0. Cần kiểm định xem điểm trung bình thực tế có khác với mục tiêu không.

Công thức một phía tôi dùng sai:

=Z.TEST(A2:A251, 8.0, 1.5)

Kết quả trả về 0.0912, tương ứng xác suất 9.12%. Nếu so sánh với mức ý nghĩa 5%, tôi kết luận không đủ bằng chứng để bác bỏ giả thuyết. Kết luận này sai.

Công thức hai phía đúng:

=2 * MIN(Z.TEST(A2:A251, 8.0, 1.5), 1 - Z.TEST(A2:A251, 8.0, 1.5))

Kết quả hai phía là 0.1824 (18.24%). Kết luận vẫn giống nhau trong trường hợp này, nhưng logic kiểm định đúng.

Lý do cần kiểm định hai phía: Câu hỏi là “điểm trung bình có khác với 8.0 không”, không phải “điểm trung bình có lớn hơn 8.0 không”. Kiểm định hai phía xem xét cả khả năng cao hơn và thấp hơn giá trị giả thuyết.

Khi nào dùng kiểm định một phía:

Tình huống 1: Bạn chỉ quan tâm một hướng. Ví dụ kiểm tra xem phương pháp mới có tăng hiệu suất hay không, không quan tâm nếu nó giảm hiệu suất.

Tình huống 2: Có lý do lý thuyết mạnh mẽ cho một hướng cụ thể trước khi thu thập dữ liệu.

XEM THÊM: Tôi Phân Tích Giá Cổ Phiếu Chính Xác Hơn Với Hàm LOGNORM.DIST

Trong thực tế kinh doanh, kiểm định hai phía an toàn và minh bạch hơn. Tôi đặt công thức hai phía thành template mặc định trong file Excel và chỉ chuyển sang một phía khi có lý do rõ ràng.

Tham số sigma thường bị bỏ qua nhưng ảnh hưởng đến ý nghĩa

Tham số thứ ba trong hàm Z.TEST là sigma, độ lệch chuẩn của tổng thể. Excel cho phép bỏ qua tham số này. Khi bỏ qua, hàm sẽ dùng độ lệch chuẩn mẫu thay thế. Tôi bỏ qua sigma trong 90% các báo cáo đầu tiên vì nghĩ nó tùy chọn và không quan trọng.

Vấn đề là khi bạn dùng độ lệch chuẩn mẫu thay vì độ lệch chuẩn tổng thể, về mặt lý thuyết bạn nên dùng kiểm định T thay vì Z. Kiểm định Z giả định bạn biết độ lệch chuẩn tổng thể một cách chính xác. Kiểm định T được thiết kế cho trường hợp phải ước lượng độ lệch chuẩn từ mẫu.

Ba trường hợp thực tế tôi xử lý:

Trường hợp 1: Dữ liệu lịch sử có sẵn. Công ty có 5 năm dữ liệu về thời gian xử lý đơn hàng từ 50,000 đơn. Độ lệch chuẩn tổng thể từ dữ liệu này là 12.5 phút. Khi khảo sát 200 đơn hàng mới, tôi dùng sigma=12.5 trong hàm Z.TEST. Đây là cách dùng chính xác.

Trường hợp 2: Chỉ có dữ liệu mẫu hiện tại. Khảo sát 150 khách hàng không có dữ liệu lịch sử. Tôi bỏ qua tham số sigma, hàm tự động tính từ mẫu. Với kích thước mẫu này, sự khác biệt giữa Z.TEST và T.TEST nhỏ (dưới 0.001 trong giá trị p), nhưng về mặt lý thuyết T.TEST chính xác hơn.

Trường hợp 3: Mẫu lớn và không có thông tin tổng thể. Với mẫu từ 300 quan sát trở lên, độ lệch chuẩn mẫu xấp xỉ rất tốt cho độ lệch chuẩn tổng thể. Tôi bỏ qua sigma và tin tưởng vào kết quả Z.TEST.

Công thức Z.TEST tính toán khi bỏ qua sigma:

Z.TEST(array, x) = 1 - NORM.S.DIST((AVERAGE(array) - x) / (STDEV(array) / SQRT(COUNT(array))), TRUE)

Công thức này dùng độ lệch chuẩn mẫu STDEV(array) thay vì sigma tổng thể. Với mẫu lớn, công thức vẫn cho kết quả chấp nhận được nhưng không nghiêm ngặt về mặt thống kê.

Nguyên tắc tôi áp dụng sau khi học được điều này:

Nếu có dữ liệu lịch sử đáng tin cậy về độ lệch chuẩn tổng thể, luôn dùng tham số sigma trong Z.TEST.
Nếu không có dữ liệu lịch sử và mẫu dưới 200, dùng T.TEST thay vì Z.TEST.
Nếu mẫu từ 200 trở lên và không có sigma tổng thể, có thể dùng Z.TEST với sigma bỏ qua, nhưng ghi chú rõ trong báo cáo.

XEM THÊM: 5 Bước Sử Dụng Hàm T.DIST.RT Thay Thế Bảng Tra Giá Trị Tới Hạn

Việc ghi chú phương pháp thống kê rõ ràng giúp tôi tránh được 3 lần phải giải thích lại kết quả với sếp khi bị hỏi tại sao kết luận khác với phân tích trước đó.

Phiên bản Excel và tên hàm thay đổi

Một chi tiết nhỏ gây nhầm lẫn: Từ Excel 2010 trở đi, Microsoft đổi tên hàm từ ZTEST thành Z.TEST (có dấu chấm). Hàm cũ ZTEST vẫn hoạt động để tương thích ngược, nhưng Microsoft khuyến nghị dùng Z.TEST cho các file mới.

Sự khác biệt giữa hai phiên bản:

Cú pháp và kết quả giống hệt nhau. Chỉ khác tên gọi. File Excel tôi nhận từ đồng nghiệp có ZTEST, file tôi tạo mới có Z.TEST. Cả hai đều tính toán chính xác.

Tương thích:

Excel 2010, 2013, 2016, 2019, 2021: Hỗ trợ cả ZTEST và Z.TEST
Excel 365: Hỗ trợ cả hai, khuyến nghị Z.TEST
Excel 2007 trở về trước: Chỉ có ZTEST

Để đảm bảo file hoạt động trên nhiều phiên bản Excel, tôi dùng Z.TEST cho các file nội bộ và ZTEST khi gửi cho đối tác không rõ phiên bản Excel họ dùng.

Quy trình quyết định nhanh: Z.TEST hay T.TEST

Sau 500 báo cáo, tôi rút ra quy trình ra quyết định trong 30 giây:

Bước 1: Kiểm tra kích thước mẫu. Nếu n < 30, dùng T.TEST không cần suy nghĩ.

Bước 2: Với n ≥ 30, hỏi bản thân có biết độ lệch chuẩn tổng thể không. Nếu có dữ liệu lịch sử đáng tin cậy về sigma, dùng Z.TEST với tham số sigma.

Bước 3: Nếu không có sigma tổng thể nhưng n ≥ 200, dùng Z.TEST bỏ qua sigma. Kết quả sẽ gần giống T.TEST.

Bước 4: Với 30 ≤ n < 200 và không có sigma tổng thể, dùng T.TEST để an toàn. Sự khác biệt không lớn nhưng T.TEST chính xác hơn về mặt lý thuyết.

Bước 5: Luôn dùng công thức hai phía trừ khi có lý do rõ ràng cho kiểm định một phía.

Quy trình này giúp tôi tránh được các lỗi phân tích mà tôi mắc phải trước đây. Thời gian sửa lại 60 báo cáo đầu tiên là 40 giờ. Đầu tư vài phút hiểu rõ sự khác biệt giữa Z.TEST và T.TEST tiết kiệm được nhiều giờ sau này.