99% Người Dùng Excel Không Cần Hàm BESSELK Nhưng 1% Còn Lại Thì Cần Gấp

Hầu hết người dùng chưa bao giờ thấy hàm BESSELK trong danh sách hàm của Excel. Ngay cả những ai làm việc với bảng tính hàng ngày thường chỉ cần VLOOKUP, SUMIF, hoặc các hàm phổ biến khác. Nhưng với kỹ sư cơ khí, nhà vật lý, và các chuyên gia kỹ thuật, BESSELK giải quyết những bài toán phức tạp mà công cụ thông thường không làm được.

Mục Lục

Hàm BESSELK Là Gì

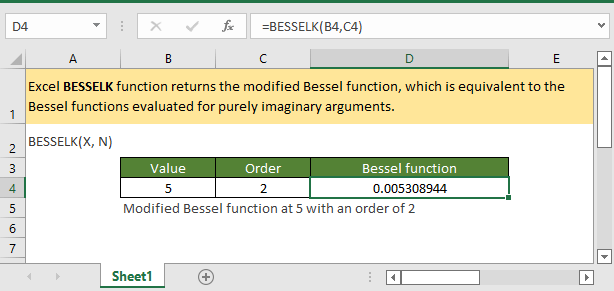
Hàm BESSELK trong Excel trả về giá trị của hàm Bessel biến đổi bậc hai, ký hiệu toán học là Kn(x). Đây là một trong bốn hàm Bessel mà Excel hỗ trợ, cùng với BESSELJ, BESSELY, và BESSELI. Các hàm này xuất hiện khi giải các phương trình vi phân trong hệ tọa độ trụ hoặc cầu.

Cú pháp cơ bản:

=BESSELK(x, n)

Trong đó:

x: Giá trị cần tính toán (phải là số dương)
n: Bậc của hàm (số nguyên không âm)

Hàm sẽ trả về giá trị số. Nếu x hoặc n không phải số, Excel trả về lỗi giá trị. Nếu n nhỏ hơn 0, hàm trả về lỗi số. Nếu n không phải số nguyên, Excel tự động làm tròn xuống thành số nguyên gần nhất.

Ví dụ, công thức =BESSELK(1.5, 2) tính giá trị hàm Bessel biến đổi bậc 2 tại điểm 1.5, trả về kết quả khoảng 0.5386.

Tại Sao Không Dùng Công Cụ Khác

Kỹ sư thường tính các giá trị Bessel bằng ba cách: tra bảng in sẵn, dùng máy tính khoa học, hoặc viết code trong phần mềm chuyên dụng. Mỗi phương pháp có hạn chế riêng.

Bảng tra cứu in trong sách giáo khoa cung cấp giá trị rời rạc. Giả sử bạn cần K2(1.5) nhưng bảng chỉ có K2(1.0) và K2(2.0), bạn phải nội suy thủ công. Với mười giá trị cần tính, việc này mất 15-20 phút và dễ nhầm lẫn.

Máy tính khoa học Casio hoặc TI có hàm Bessel nhưng độ chính xác giới hạn ở 10-12 chữ số. Đối với tính toán kỹ thuật cần độ chính xác cao, điều này không đủ. Hơn nữa, bạn phải nhập từng giá trị một, không thể tính hàng loạt.

Phần mềm chuyên dụng như MATLAB hoặc Python với thư viện SciPy tính toán chính xác nhưng đòi hỏi giấy phép riêng hoặc kiến thức lập trình. Viết script đơn giản cũng mất 10-15 phút, chưa kể thời gian cài đặt và cấu hình môi trường.

Excel khác biệt ở chỗ hàm BESSELK có sẵn từ phiên bản 2007 trở đi. Không cần cài thêm, không cần lập trình. Nhập công thức, kéo xuống hàng trăm ô, kết quả hiện ngay lập tức. Độ chính xác đủ cho hầu hết ứng dụng kỹ thuật thực tế.

XEM THÊM: Cách Dùng Hàm DEC2BIN Để Chuyển Số Thập Phân Sang Nhị Phân Trong 3 Bước

So sánh thời gian tính 50 giá trị Bessel:

Tra bảng + nội suy thủ công: 45 phút
Máy tính khoa học: 25 phút
Viết code Python: 20 phút (lần đầu), 2 phút (lần sau)
Excel: 3 phút (lần đầu), 30 giây (lần sau)

Với Excel, bạn sao chép công thức sang các ô khác, thay đổi tham số, và kết quả cập nhật tự động. Điều này đặc biệt hữu ích khi phải thử nhiều giá trị hoặc kiểm tra độ nhạy của kết quả.

Ứng Dụng Trong Truyền Nhiệt

Bài toán truyền nhiệt trong ống trụ là ví dụ điển hình. Một ống kim loại bán kính 5cm, chiều dày thành 1cm, nhiệt độ bề mặt trong 200°C, bề mặt ngoài 50°C. Yêu cầu tính phân bố nhiệt độ tại các điểm bên trong thành ống.

Phương trình truyền nhiệt trong tọa độ trụ có nghiệm dạng tổ hợp các hàm Bessel. Đối với hình học ống trụ, hàm BESSELK xuất hiện tự nhiên trong công thức. Không có hàm này, bạn phải dùng phương pháp số gần đúng hoặc tra bảng.

Giả sử cần tính nhiệt độ tại 20 vị trí khác nhau theo bán kính. Mỗi vị trí đòi hỏi một giá trị BESSELK khác nhau. Công thức trong ô B2 có thể là:

=200 - (200-50) * (BESSELK(A2/5, 0) - BESSELK(5/5, 0)) / (BESSELK(6/5, 0) - BESSELK(5/5, 0))

Trong đó A2 chứa bán kính cần tính. Kéo công thức xuống 20 hàng, kết quả hiện ngay. Biểu đồ nhiệt độ theo bán kính được tạo trong vòng 1 phút.

Phương pháp này áp dụng cho các bài toán tương tự: truyền nhiệt trong sợi quang, phân bố ứng suất trong trục quay, hoặc truyền sóng trong ống dẫn sóng hình trụ. Bất kỳ hệ thống nào có đối xứng trụ đều có khả năng cần hàm Bessel.

Phân Tích Dao Động Và Sóng

Dao động của màng tròn, như mặt trống, được mô tả bởi các hàm Bessel. Khi phân tích chế độ dao động, các hàm BESSELJ và BESSELK xuất hiện trong biểu thức tần số riêng. Kỹ sư âm thanh hoặc thiết kế nhạc cụ cần tính các giá trị này để dự đoán âm sắc.

Trong truyền sóng điện từ qua ống dẫn sóng đồng trục, phân bố trường điện và từ cũng liên quan đến hàm Bessel. Tính toán trở kháng đặc tính hoặc tần số cắt yêu cầu đánh giá các hàm này tại nhiều điểm. Excel xử lý nhanh hơn nhiều so với tra bảng thủ công.

Một ví dụ cụ thể: tính tần số cắt của chế độ TE11 trong ống dẫn sóng hình trụ. Công thức liên quan đến nghiệm của phương trình có hàm Bessel. Thay vì giải phương trình bằng phương pháp lặp phức tạp, bạn có thể tạo bảng các giá trị BESSELJ với tham số thay đổi, sau đó tìm điểm giao với đường ngang bằng biểu đồ Excel.

XEM THÊM: Hướng Dẫn Chi Tiết Hàm BITRSHIFT: Cú Pháp, Ví Dụ Và Ứng Dụng Thực Tế

Phương pháp này không thay thế hoàn toàn phần mềm mô phỏng chuyên nghiệp như COMSOL hoặc HFSS, nhưng phù hợp cho tính toán nhanh, kiểm tra kết quả, hoặc ước lượng ban đầu trước khi chạy mô phỏng tốn thời gian.

Tính Toán Ứng Suất Nhiệt

Ứng suất nhiệt trong các chi tiết hình trụ, như trục động cơ hoặc ống trao đổi nhiệt, phụ thuộc vào phân bố nhiệt độ không đồng đều. Khi một phần của trục nóng hơn phần khác, vật liệu giãn nở không đều, tạo ra ứng suất bên trong.

Phương trình ứng suất nhiệt trong hệ tọa độ trụ có nghiệm chứa hàm Bessel biến đổi. Đối với trục đặc hoặc ống rỗng chịu gradient nhiệt độ theo bán kính, hàm BESSELK xuất hiện trong biểu thức ứng suất tiếp tuyến và ứng suất hướng kính.

Giả sử một trục thép đường kính 10cm bị nung nóng từ tâm. Bề mặt được làm mát bằng nước. Nhiệt độ tâm 300°C, bề mặt 80°C. Cần tính ứng suất tối đa để kiểm tra liệu vật liệu có bị biến dạng dẻo hay không.

Công thức ứng suất chứa tích phân của hàm Bessel nhân với nhiệt độ. Excel có thể tính gần đúng bằng cách chia miền tích phân thành các đoạn nhỏ, tính giá trị BESSELK tại mỗi điểm, rồi cộng lại theo quy tắc hình thang. Với 50 điểm chia, sai số dưới 1%, chấp nhận được cho phân tích sơ bộ.

Kết quả cho thấy ứng suất tối đa xảy ra không phải ở tâm hay bề mặt mà ở vị trí trung gian, khoảng 3cm từ tâm. Thông tin này giúp kỹ sư quyết định cần xử lý nhiệt thế nào để tránh vết nứt.

Hàm BESSELK So Với Các Hàm Bessel Khác

Excel cung cấp bốn hàm Bessel, mỗi loại phục vụ mục đích riêng. BESSELJ là hàm Bessel loại một, giải bài toán trong miền hữu hạn với điều kiện biên cố định. BESSELY là hàm Bessel loại hai, xuất hiện khi có kỳ dị tại gốc tọa độ. BESSELI là hàm Bessel biến đổi loại một, dùng cho bài toán có hàm số tăng theo bán kính.

BESSELK khác ở chỗ nó giảm mũ khi biến số tăng. Điều này phù hợp với các bài toán vật lý có giá trị tiệm cận bằng không khi ra xa, như trường điện từ trong môi trường hấp thụ hoặc nhiệt độ trong vật thể bán vô hạn.

Chọn hàm nào phụ thuộc vào dạng phương trình và điều kiện biên. Nếu nghiệm phải hữu hạn tại gốc, dùng BESSELJ hoặc BESSELI. Nếu nghiệm phải triệt tiêu ở vô cùng, dùng BESSELK. Đọc tài liệu chuyên ngành hoặc sách giáo khoa phương trình vi phân để xác định chính xác.

XEM THÊM: Hàm GESTEP Giúp Tôi Đếm Dữ Liệu Nhanh Gấp 5 Lần So Với COUNTIF

Một mẹo là kiểm tra đơn vị và dấu trong công thức vật lý. Hàm Bessel biến đổi thường đi kèm với biến số có thứ nguyên ngược với độ dài, như hằng số tắt dần hoặc số sóng ảo. Nếu thấy mẫu số này, nhiều khả năng cần BESSELK thay vì BESSELJ.

Lưu Ý Khi Sử Dụng

Hàm BESSELK chỉ chấp nhận giá trị x dương. Nếu nhập số âm hoặc bằng không, Excel trả về lỗi số. Điều này hợp lý về mặt toán học vì hàm Kn(x) không xác định hoặc phân kỳ tại x bằng 0.

Đối với bậc n, Excel chỉ hỗ trợ số nguyên không âm. Nếu nhập n âm, hàm báo lỗi. Nếu nhập n thập phân như 2.7, Excel tự động làm tròn xuống thành 2. Hành vi này khác với một số phần mềm toán học khác cho phép bậc thực hoặc phức.

Độ chính xác của Excel đủ cho hầu hết ứng dụng kỹ thuật nhưng có giới hạn. Với x rất lớn hoặc rất nhỏ, sai số số học có thể tích lũy. Nếu cần độ chính xác cao hơn 12 chữ số thập phân, nên chuyển sang phần mềm tính toán số chuyên dụng như Mathematica hoặc Maple.

Một hạn chế khác là Excel không tính được đạo hàm hoặc tích phân của hàm Bessel. Nếu bài toán yêu cầu đạo hàm K’n(x), bạn phải tính gần đúng bằng sai phân hữu hạn hoặc dùng công thức đệ quy giữa các bậc khác nhau.

Công thức đệ quy hữu ích: Kn-1(x) – Kn+1(x) = -2K’n(x). Từ đây, có thể tính đạo hàm nếu biết hai giá trị hàm ở bậc lân cận. Excel dễ dàng tính BESSELK(x, n-1) và BESSELK(x, n+1), sau đó áp dụng công thức.

Phiên Bản Và Tính Tương Thích

Hàm BESSELK có sẵn từ Excel 2007 trở đi. Các phiên bản cũ hơn như Excel 2003 hoặc Excel 2000 không hỗ trợ. Nếu mở file chứa BESSELK trong Excel 2003, công thức sẽ hiển thị lỗi tên.

Các phiên bản hiện đại bao gồm Excel 2010, 2013, 2016, 2019, 2021 và Microsoft 365 đều hỗ trợ đầy đủ. Hàm cũng hoạt động trong Excel trên web và Excel trên thiết bị di động, mặc dù giao diện nhập công thức có thể khác chút ít.

Đối với những ai không dùng Excel hoặc cần tính toán phức tạp hơn, các lựa chọn thay thế bao gồm LibreOffice Calc (có hàm Bessel tương tự), Google Sheets (chưa hỗ trợ trực tiếp nhưng có thể dùng Apps Script gọi thư viện bên ngoài), hoặc phần mềm tính toán số như MATLAB, Octave, Python với NumPy/SciPy.

Đối với các nhà nghiên cứu hoặc kỹ sư làm việc trong môi trường hạn chế phần mềm, Excel là công cụ phổ biến nhất có khả năng tính hàm Bessel mà không cần cài thêm gì. Điều này giải thích tại sao, mặc dù chỉ 1% người dùng cần, những người đó thực sự phụ thuộc vào nó hàng ngày.