Hàm ERF.PRECISE Trong Excel 2010: Cú Pháp Ví Dụ Và Lỗi Thường Gặp

Hàm ERF.PRECISE xuất hiện từ Excel 2010 nhưng ít người biết đến. Đây là hàm kỹ thuật tính hàm sai số tích phân từ 0 đến một giá trị bất kỳ, thường dùng trong phân tích thống kê và tính toán liên quan đến phân phối chuẩn. Nếu bạn làm việc với dữ liệu thống kê hoặc các bài toán kỹ thuật, hàm này có thể hữu ích hơn bạn nghĩ.

Mục Lục

Hàm ERF.PRECISE tính toán gì

ERF.PRECISE trả về giá trị hàm sai số Gauss tích phân từ 0 đến một số x bất kỳ. Trong thống kê, hàm này biểu thị xác suất một biến ngẫu nhiên có phân phối chuẩn với trung bình 0 và độ lệch chuẩn 1/√2 rơi vào khoảng từ -x đến x.

Hàm này thuộc nhóm Engineering Functions và thường được dùng trong các tính toán liên quan đến lý thuyết xác suất, vật lý toán học, và giải phương trình vi phân. Kết quả trả về luôn nằm trong khoảng từ -1 đến 1.

Công thức toán học:

ERF.PRECISE(x) = (2/√π) × ∫₀ˣ e^(-t²) dt

Cú pháp và tham số

Cú pháp của hàm cực kỳ đơn giản với chỉ một tham số duy nhất:

=ERF.PRECISE(x)

Tham số:

x (bắt buộc): Giới hạn dưới để tính tích phân hàm sai số. Đây là giá trị số mà bạn muốn tính hàm ERF.PRECISE.

Không giống hàm ERF thông thường, ERF.PRECISE không có tham số upper_limit. Hàm luôn tính từ 0 đến x.

XEM THÊM: Hàm IMDIV: Công Cụ Ẩn Giúp Kỹ Sư Tiết Kiệm Hàng Giờ Tính Toán

Lưu ý quan trọng:

Nếu x không phải là số, hàm trả về lỗi #VALUE!
Nếu x = 0, hàm trả về 0
Nếu x > 0, kết quả dương
Nếu x < 0, kết quả âm (hàm ERF.PRECISE là hàm lẻ)

Ví dụ thực tế

Dưới đây là các ví dụ cụ thể cho từng trường hợp:

Ví dụ 1: Giá trị dương

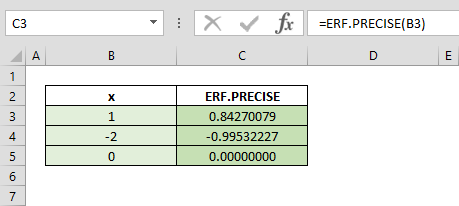
Trong ô A1, nhập: =ERF.PRECISE(1)

Kết quả: 0.842700792949715

Con số này có nghĩa là xác suất một biến ngẫu nhiên chuẩn rơi trong khoảng từ -1 đến 1 là khoảng 84.27%.

Ví dụ 2: Giá trị âm

Trong ô A2, nhập: =ERF.PRECISE(-0.5)

Kết quả: -0.520499877813047

Giá trị âm vì hàm ERF.PRECISE là hàm lẻ, có nghĩa ERF.PRECISE(-x) = -ERF.PRECISE(x).

Ví dụ 3: Tham chiếu ô

Giả sử ô B1 chứa giá trị 0.745, trong ô C1 nhập:

=ERF.PRECISE(B1)

Kết quả: 0.707853852557087

Cách này tiện lợi hơn khi bạn cần tính hàm ERF.PRECISE cho nhiều giá trị khác nhau trong bảng tính.

Ví dụ 4: Bảng tính nhiều giá trị

A	B	C
Giá trị x	Công thức	Kết quả ERF.PRECISE
0	=ERF.PRECISE(A2)	0
0.25	=ERF.PRECISE(A3)	0.276326
0.5	=ERF.PRECISE(A4)	0.520500
1	=ERF.PRECISE(A5)	0.842701
1.5	=ERF.PRECISE(A6)	0.966105
2	=ERF.PRECISE(A7)	0.995322

Copy công thức từ ô B2 xuống các ô bên dưới để tính hàm ERF.PRECISE cho nhiều giá trị cùng lúc.

Phân biệt ERF và ERF.PRECISE

Nhiều người nhầm lẫn giữa hai hàm ERF và ERF.PRECISE. Dưới đây là sự khác biệt chính:

Hàm ERF:

Cú pháp: =ERF(lower_limit, [upper_limit])
Có 2 tham số (upper_limit là tùy chọn)
Nếu bỏ qua upper_limit, ERF tính từ 0 đến lower_limit
Có sẵn từ Excel 2007

XEM THÊM: Cách Sử Dụng Tham Số Places Trong DEC2HEX Để Định Dạng Kết Quả Chuẩn

Hàm ERF.PRECISE:

Cú pháp: =ERF.PRECISE(x)
Chỉ có 1 tham số
Luôn tính từ 0 đến x
Có từ Excel 2010 trở đi
Độ chính xác cao hơn trong một số trường hợp

Khi nào dùng ERF.PRECISE thay vì ERF?

Sử dụng ERF.PRECISE khi:

Bạn chỉ cần tính từ 0 đến một giá trị nhất định (không cần upper_limit)
Cần độ chính xác cao hơn cho các tính toán khoa học
Muốn đảm bảo tính tương thích ngược với các version Excel mới hơn

Trong hầu hết trường hợp, nếu bạn bỏ qua tham số upper_limit trong hàm ERF, hai hàm sẽ cho kết quả giống hệt nhau. Ví dụ:

=ERF(1) = ERF.PRECISE(1) = 0.842700792949715

Lỗi #VALUE! và cách khắc phục

Lỗi phổ biến nhất khi dùng ERF.PRECISE là lỗi #VALUE!. Lỗi này xảy ra khi tham số x không phải là giá trị số.

Các trường hợp gây lỗi #VALUE!:

Nhập text thay vì số:

=ERF.PRECISE("abc")  → #VALUE!

Ô tham chiếu chứa text:

Ô A1 chứa: "không phải số"
=ERF.PRECISE(A1)  → #VALUE!

Ô trống hoặc ô chứa lỗi:

Ô B1 trống hoặc chứa lỗi #DIV/0!
=ERF.PRECISE(B1)  → #VALUE!

Cách khắc phục:

Sử dụng hàm ISNUMBER để kiểm tra trước khi tính:

=IF(ISNUMBER(A1), ERF.PRECISE(A1), "Giá trị không hợp lệ")

Hoặc dùng IFERROR để xử lý lỗi:

=IFERROR(ERF.PRECISE(A1), 0)

Công thức này sẽ trả về 0 nếu A1 không phải là số, giúp tránh lỗi hiển thị trong bảng tính.

Ứng dụng trong phân tích thống kê

ERF.PRECISE hữu ích trong nhiều tình huống thực tế:

1. Tính xác suất phân phối chuẩn:

Khi bạn có một biến ngẫu nhiên Z tuân theo phân phối chuẩn chuẩn hóa, bạn có thể tính xác suất Z rơi vào khoảng [-x, x] bằng ERF.PRECISE.

XEM THÊM: Hướng Dẫn Chi Tiết Hàm BITOR Excel 2013 Với Ví Dụ Cụ Thể

Ví dụ: Tính xác suất một giá trị rơi trong khoảng 1 độ lệch chuẩn:

=ERF.PRECISE(1/SQRT(2))  → 0.682689

Kết quả cho thấy khoảng 68.27% dữ liệu nằm trong 1 độ lệch chuẩn, đúng với quy tắc 68-95-99.7.

2. Kiểm định giả thuyết:

Trong kiểm định thống kê, hàm ERF.PRECISE có thể tính giá trị p-value cho các test liên quan đến phân phối chuẩn.

3. Phân tích rủi ro tài chính:

Trong mô hình Black-Scholes và các mô hình định giá quyền chọn, hàm sai số là một phần quan trọng của công thức.

4. Kỹ thuật và vật lý:

ERF.PRECISE xuất hiện trong nghiệm của phương trình nhiệt, phương trình khuếch tán, và nhiều bài toán vật lý toán học khác.

Tương thích và phiên bản

Hàm ERF.PRECISE có sẵn trong các phiên bản Excel sau:

Excel 2010 trở đi
Excel 2013, 2016, 2019, 2021
Excel 365 (Microsoft 365)
Excel cho Mac 2011 trở lên
Excel cho web

Nếu bạn mở file chứa ERF.PRECISE trong Excel 2007 hoặc cũ hơn, hàm sẽ trả về lỗi #NAME! vì không được hỗ trợ. Trong trường hợp này, sử dụng hàm ERF thay thế với cú pháp =ERF(x) sẽ cho kết quả tương tự.

Đối với các tính toán yêu cầu độ chính xác cao, ERF.PRECISE là lựa chọn tốt hơn trong Excel 2010 trở lên. Hàm này đặc biệt hữu ích khi làm việc với dữ liệu thống kê, mô hình toán học, hoặc các bài toán kỹ thuật liên quan đến phân phối chuẩn. Nhớ kiểm tra giá trị đầu vào để tránh lỗi #VALUE! và luôn sử dụng tham chiếu ô thay vì hard-code số khi có thể để bảng tính dễ cập nhật hơn.