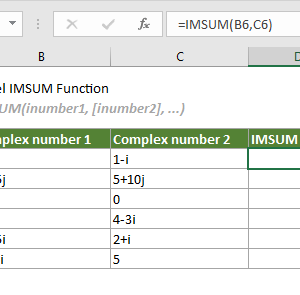
Nếu bạn đang tính toán trở kháng trong Excel bằng công thức thủ công, mỗi phép chia số phức có thể mất đến 2 phút để nhập xong. Hàm IMDIV hoàn thành cùng phép tính trong 5 giây với độ chính xác tuyệt đối. Công cụ này nằm yên trong nhóm hàm kỹ thuật của Excel, nhưng ít kỹ sư biết đến nó.
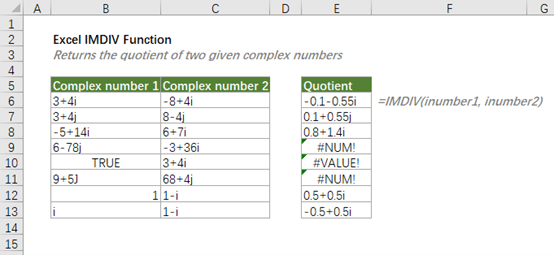
Hàm IMDIV tính gì
Hàm IMDIV thực hiện phép chia hai số phức và trả về kết quả dưới dạng văn bản theo định dạng x+yi hoặc x+yj. Đây là hàm thuộc nhóm Engineering Functions trong Excel, có sẵn từ Excel 2007 trở đi.
Cú pháp cơ bản:
=IMDIV(inumber1, inumber2)
Trong đó inumber1 là số phức bị chia, inumber2 là số phức chia. Cả hai tham số phải được nhập trong dấu ngoặc kép nếu là giá trị trực tiếp, ví dụ: =IMDIV("5+3i","2+i") trả về kết quả 1.5+0.5i.
Hàm này tuân theo công thức toán học chuẩn cho phép chia số phức: (a+bi)/(c+di) = [(ac+bd)/(c²+d²)] + [(bc-ad)/(c²+d²)]i. Excel tự động xử lý toàn bộ phép tính phức tạp này trong một hàm duy nhất.
Ứng dụng thực tế trong tính toán trở kháng
Kỹ sư điện làm việc với trở kháng mạch điện phải chia số phức liên tục. Trở kháng có dạng Z = R + jX, trong đó R là điện trở và X là điện kháng. Khi phân tích mạch xoay chiều, phép chia trở kháng xuất hiện trong nhiều bài toán.
Ví dụ mạch RLC: Tính tổng trở của mạch song song với Z1 = 10+5j và Z2 = 8-3j. Công thức tổng trở song song là 1/Z = 1/Z1 + 1/Z2. Để tính 1/Z1, bạn dùng =IMDIV("1","10+5j") thay vì tính thủ công (10-5j)/125.
Tính toán công suất phức: Khi biết điện áp U = 220+0j và dòng điện I = 5+3j, công suất biểu kiến S = U×I*. Để tìm trở kháng Z = U/I, công thức =IMDIV("220","5+3j") cho kết quả ngay lập tức.
Phối hợp trở kháng: Trong thiết kế mạch RF, bạn cần tính hệ số phản xạ Γ = (ZL-Z0)/(ZL+Z0). Với ZL = 75+20j và Z0 = 50, công thức =IMDIV(IMSUB("75+20j","50"),IMSUM("75+20j","50")) tự động tính toàn bộ biểu thức trong một ô.
Tôi thường dùng hàm này khi phân tích mạch lọc tần số. Thay vì 10 phút cho một bảng tính 20 hàng, toàn bộ việc tính toán hoàn tất trong 2 phút nhờ công thức có thể kéo xuống.
So sánh với phương pháp thủ công
Tính thủ công phép chia (4+3j)/(2+j) yêu cầu bạn nhân cả tử và mẫu với liên hợp của mẫu. Quy trình gồm 5 bước:
- Tìm liên hợp của mẫu: 2-j
- Nhân tử số: (4+3j)(2-j) = 8-4j+6j-3j² = 8+2j+3 = 11+2j
- Nhân mẫu: (2+j)(2-j) = 4-j² = 4+1 = 5
- Chia phần thực: 11/5 = 2.2
- Chia phần ảo: 2/5 = 0.4
Kết quả cuối cùng: 2.2+0.4j. Với Excel, công thức =IMDIV("4+3j","2+j") cho cùng kết quả mà không cần bất kỳ bước trung gian nào.
Độ chính xác: Hàm IMDIV duy trì độ chính xác đến 15 chữ số thập phân. Tính tay thường làm tròn sau 2-3 chữ số, gây sai số tích lũy trong chuỗi phép tính. Một bảng tính trở kháng 50 hàng có thể có sai số lên đến 5% nếu làm tròn mỗi bước.
Tốc độ: Nhập một công thức IMDIV mất 5 giây. Tính tay cùng phép toán mất 90-120 giây tùy thuộc kỹ năng. Trong một dự án thiết kế mạch với 200 phép tính, hàm IMDIV tiết kiệm khoảng 6 giờ so với phương pháp truyền thống.
Kết hợp với các hàm số phức khác
Hàm IMDIV hoạt động mạnh mẽ khi kết hợp với các hàm Engineering khác. Hàm COMPLEX chuyển đổi hệ số thực và ảo riêng lẻ thành số phức: =COMPLEX(3,4) tạo ra “3+4i”.
Xây dựng công thức phức hợp: Để tính (5+2j)/(3-j) + 4+3j, sử dụng =IMSUM(IMDIV("5+2j","3-j"),"4+3j"). Hàm IMSUM cộng kết quả của IMDIV với số phức thứ hai.
Tính modun trở kháng: Sau khi tính trở kháng bằng IMDIV, dùng IMABS để lấy độ lớn: =IMABS(IMDIV("10+5j","2+j")) trả về giá trị vô hướng của trở kháng.
Chuyển đổi dạng cực: Công thức =IMARGUMENT(IMDIV("20+15j","5-3j")) tính góc pha của kết quả chia, hữu ích khi phân tích độ lệch pha trong mạch điện.
Lưu ý rằng tất cả số phức trong cùng một chuỗi tính toán phải dùng chung hậu tố i hoặc j. Trộn lẫn “3+2i” và “5-4j” trong cùng công thức sẽ trả về lỗi giá trị.
Các lỗi thường gặp
Hàm IMDIV trả về lỗi khi gặp dữ liệu không hợp lệ. Lỗi phổ biến nhất là khi số phức không được đặt trong dấu ngoặc kép. =IMDIV(3+2i,1+i) sẽ báo lỗi vì Excel cố gắng đọc 3+2i như một biểu thức thay vì chuỗi ký tự.
Lỗi dấu phân cách: Số phức phải viết liền không có khoảng trắng. “3 + 2i” sẽ không được nhận dạng, phải viết “3+2i” hoặc “3-2i” tùy dấu của phần ảo.
Lỗi hậu tố: Chỉ chấp nhận chữ thường “i” hoặc “j”. Sử dụng chữ hoa “I” hoặc “J” gây lỗi giá trị. Hàm IMDIV phân biệt chính xác chữ hoa và chữ thường ở hậu tố này.
Chia cho số không: =IMDIV("5+3j","0") trả về lỗi chia cho không như mong đợi. Tuy nhiên lưu ý rằng “0+0j” cũng được coi là số không và gây lỗi tương tự.
Để xử lý lỗi trong bảng tính lớn, bọc hàm trong IFERROR: =IFERROR(IMDIV(A1,B1),"Lỗi dữ liệu") hiển thị thông báo thay vì mã lỗi khi gặp giá trị không hợp lệ.
Khi nào nên dùng hàm IMDIV
Hàm này không phải cho mọi tình huống. Đối với phép chia số thực đơn giản, công thức chia thông thường nhanh và rõ ràng hơn. IMDIV chỉ cần thiết khi làm việc với số có phần ảo.
Các tình huống phù hợp:
- Phân tích mạch xoay chiều với trở kháng phức
- Xử lý tín hiệu trong miền tần số
- Tính toán đường truyền RF
- Thiết kế bộ lọc điện tử
- Mô phỏng hệ thống điều khiển
Khi không nên dùng:
- Tính toán mạch một chiều (chỉ có điện trở thực)
- Số liệu tài chính không có phần ảo
- Phép chia số nguyên hoặc thập phân thông thường
Excel 2019 và các phiên bản mới hơn hỗ trợ đầy đủ hàm này. Excel 2016 trở về trước cần cài đặt Analysis ToolPak để kích hoạt nhóm hàm Engineering. Phiên bản Excel trên web và Excel cho Mac đều hỗ trợ IMDIV mà không cần add-in bổ sung.
Nếu bạn thường xuyên làm việc với số phức, việc làm quen với IMDIV và các hàm số phức khác trong Excel sẽ tăng năng suất đáng kể. Một bảng tính trở kháng mạch điện có thể hoàn thành trong 15 phút thay vì 2 giờ với công thức phù hợp.