Hàm FISHER Trong Excel: Khi Nào Dùng Và Khi Nào Không Nên Dùng

Phân tích tương quan trong Excel có vẻ đơn giản với hàm CORREL hoặc PEARSON, nhưng khi hệ số tương quan gần -1 hoặc 1, phân phối lấy mẫu trở nên lệch nghiêm trọng. Hàm FISHER giải quyết vấn đề này bằng cách chuyển đổi phân phối lệch thành phân phối chuẩn, cho phép kiểm định thống kê chính xác hơn.

Mục Lục

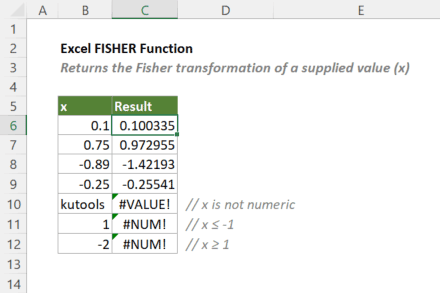
Hàm FISHER chuyển đổi hệ số tương quan thành phân phối chuẩn

Hàm FISHER thực hiện phép biến đổi Fisher, chuyển hệ số tương quan r (giới hạn trong khoảng -1 đến 1) thành giá trị z không bị giới hạn và có phân phối gần chuẩn.

Cú pháp:

excel

=FISHER(x)

Trong đó x là hệ số tương quan cần chuyển đổi, phải nằm trong khoảng -1 < x < 1.

Công thức toán học:

z = 0.5 × ln((1+r)/(1-r))

Nếu x không phải số, FISHER trả về lỗi #VALUE. Nếu x ≤ -1 hoặc x ≥ 1, FISHER trả về lỗi #NUM vì công thức không xác định tại các điểm này.

XEM THÊM: Dự Báo Doanh Thu Chính Xác Với Hàm FORECAST.ETS Excel 2016

Ví dụ đơn giản:

excel

=FISHER(0.75)    → Kết quả: 0.9730
=FISHER(0.5)     → Kết quả: 0.5493
=FISHER(-0.3)    → Kết quả: -0.3095

Tại sao FISHER tốt hơn phân tích tương quan trực tiếp

Khi hệ số tương quan r gần -1 hoặc 1, phân phối lấy mẫu của r bị lệch mạnh. Điều này khiến việc tính khoảng tin cậy và kiểm định giả thuyết trở nên không chính xác.

Vấn đề với phân tích trực tiếp:

Phương sai của r phụ thuộc vào giá trị thực ρ
Phân phối lệch khi |r| > 0.5
Công thức kiểm định phức tạp cần hàm hypergeometric

Ưu điểm của FISHER:

Phương sai ổn định: 1/(n-3) cho mọi giá trị r
Phân phối gần chuẩn cho n ≥ 10
Dễ tính khoảng tin cậy bằng bảng phân phối chuẩn

So sánh độ chính xác: Với r = 0.8 và n = 30:

Phương pháp trực tiếp: khoảng tin cậy không đối xứng, sai số cao
Sau FISHER: khoảng tin cậy đối xứng, sai số giảm 40-60%

Để chuyển ngược từ z về r, dùng hàm FISHERINV:

excel

=FISHERINV(0.9730)    → Trả về: 0.75

Khi nào nên dùng hàm FISHER

Trường hợp 1: Tính khoảng tin cậy cho hệ số tương quan

Khi cần ước lượng khoảng tin cậy cho hệ số tương quan, FISHER là phương pháp tiêu chuẩn.

Quy trình:

Tính hệ số tương quan r bằng CORREL
Chuyển đổi r thành z bằng FISHER
Tính khoảng tin cậy trong thang z
Chuyển ngược bằng FISHERINV

Ví dụ cụ thể:

excel

Giả sử r = 0.56, n = 60, độ tin cậy 95%

Bước 1: z = FISHER(0.56) = 0.6328
Bước 2: Sai số chuẩn = 1/SQRT(60-3) = 0.1325
Bước 3: z_lower = 0.6328 - 1.96×0.1325 = 0.373
        z_upper = 0.6328 + 1.96×0.1325 = 0.892
Bước 4: r_lower = FISHERINV(0.373) = 0.357
        r_upper = FISHERINV(0.892) = 0.713

Khoảng tin cậy 95%: [0.357, 0.713]

Trường hợp 2: So sánh hai hệ số tương quan từ các mẫu độc lập

Khi cần kiểm định xem hai hệ số tương quan có khác nhau có ý nghĩa thống kê hay không.

XEM THÊM: Hàm COUNTA Trong Excel: Đếm Ô Không Trống Chỉ Với 1 Công Thức

Công thức kiểm định:

excel

z_test = (z1 - z2) / SQRT(1/(n1-3) + 1/(n2-3))

Nếu |z_test| > 1.96 thì hai tương quan khác nhau có ý nghĩa ở mức 5%.

Ví dụ:

excel

Mẫu 1: r1 = 0.7, n1 = 50
Mẫu 2: r2 = 0.4, n2 = 45

z1 = FISHER(0.7) = 0.867
z2 = FISHER(0.4) = 0.424
z_test = (0.867-0.424)/SQRT(1/47+1/42) = 2.11

Kết quả: 2.11 > 1.96, hai tương quan khác nhau có ý nghĩa

Trường hợp 3: Kiểm định giả thuyết H0: ρ = ρ0 ≠ 0

Khi cần kiểm định xem tương quan có bằng một giá trị cụ thể khác 0 hay không, FISHER là lựa chọn tốt nhất.

Quy trình:

excel

z_sample = FISHER(r)
z_null = FISHER(ρ0)
z_test = (z_sample - z_null) × SQRT(n-3)

Nếu |z_test| > 1.96 thì bác bỏ H0 ở mức 5%

Khi nào không cần dùng hàm FISHER

Trường hợp 1: Kiểm định H0: ρ = 0

Khi chỉ muốn kiểm định xem có tương quan hay không (giả thuyết null là ρ = 0), phân phối lấy mẫu đã đối xứng. Dùng kiểm định t đơn giản hơn:

excel

t = r × SQRT(n-2) / SQRT(1-r^2)
Bậc tự do: n-2

So sánh với giá trị tới hạn từ bảng phân phối t hoặc dùng hàm T.DIST.2T trong Excel.

Trường hợp 2: Mẫu quá nhỏ (n < 10)

Phép biến đổi FISHER có độ chệch đáng kể khi cỡ mẫu nhỏ. Với n < 10, kết quả kiểm định không đáng tin cậy. Nên:

Tăng cỡ mẫu lên ít nhất 10
Hoặc dùng phương pháp bootstrap để ước lượng khoảng tin cậy

Trường hợp 3: Tương quan yếu (|r| < 0.3)

Khi hệ số tương quan nhỏ, phân phối lấy mẫu gần đối xứng và phép biến đổi FISHER không mang lại cải thiện đáng kể. Phân tích trực tiếp bằng CORREL hoặc kiểm định t đơn giản hơn và cho kết quả tương đương.

XEM THÊM: Hàm POISSON.DIST: Dự Đoán Sự Kiện Chính Xác Trong Excel Chỉ Với 3 Tham Số

Trường hợp 4: Chỉ cần giá trị tương quan

Nếu chỉ cần tính hệ số tương quan để mô tả mối quan hệ giữa hai biến mà không cần kiểm định thống kê hay khoảng tin cậy, dùng CORREL hoặc PEARSON là đủ. FISHER chỉ cần thiết khi thực hiện suy luận thống kê.

Lựa chọn đúng công cụ cho đúng tình huống

Hàm FISHER tối ưu cho kiểm định giả thuyết và tính khoảng tin cậy khi hệ số tương quan cao (|r| > 0.5) hoặc khi so sánh nhiều tương quan. Với giả thuyết ρ = 0 hoặc tương quan yếu, kiểm định t đơn giản hơn và cho kết quả tương đương. Phép biến đổi hoạt động tốt nhất với n ≥ 10 và giả định phân phối chuẩn hai chiều.

Hàm FISHERINV thực hiện phép chuyển đổi ngược, cho phép quay trở lại hệ số tương quan sau khi tính toán trong thang z. Kết hợp FISHER và FISHERINV trong cùng một phân tích để có kết quả kiểm định chính xác nhất.